Представим, что получилось собрать такой набор из 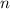 чисел, причем
чисел, причем 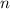 больше или равно
больше или равно 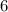 .
.
По условию, ровно  число делится на
число делится на 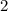 ("все, кроме одного числа, делятся на
("все, кроме одного числа, делятся на 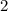 "), и ровно
"), и ровно 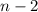 чисел делятся на
чисел делятся на 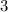 ("все, кроме двух чисел, делятся на
("все, кроме двух чисел, делятся на 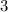 "). Это означает, что на
"). Это означает, что на 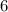 могут делиться максимум
могут делиться максимум 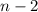 числа (когда все числа, делящиеся на
числа (когда все числа, делящиеся на 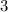 также делятся на
также делятся на 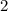 ), а минимум -
), а минимум - 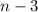 числа (когда в наборе есть одно число, делящееся на
числа (когда в наборе есть одно число, делящееся на 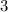 , но не делящееся на
, но не делящееся на 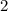 ).
).
Но нам сказано, что на 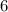 должны делиться ровно
должны делиться ровно 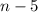 чисел, а остальные
чисел, а остальные 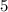 чисел на
чисел на 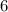 не делятся. Но выходит, что на
не делятся. Но выходит, что на 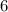 не делятся либо
не делятся либо 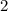 числа, либо
числа, либо 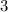 числа (но не
числа (но не 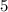 чисел).
чисел).
Значит, 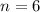 - такое невозможно.
- такое невозможно.
При этом 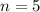 уже имеет место быть (во всяком случае, мне так кажется). В этом случае набор чисел будет, например, такой:
уже имеет место быть (во всяком случае, мне так кажется). В этом случае набор чисел будет, например, такой: 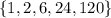 .
.
Пошаговое объяснение:
Из условия непонятно присутствуют или отсутствуют 4 учащихся.
Если только 4 учащихся присутствуют на уроке.
(100%·4)/30=13 1/3% учащихся на уроке присутствуют.
Тогда на уроке отсутствуют:
100%-13 1/3%=99 3/3 -13 1/3=86 2/3% учащихся.
(1·86 2/3)/100%=(260/3)/100=260/300=13/15 часть учащихся на уроке отсутствует.
Если 4 учащихся отсутствуют на уроке.
(100%·(30-4))/30=260/3=86 2/3% учащихся на уроке присутствуют.
Тогда на уроке отсутствуют:
100%-86 2/3%=99 3/3 -86 2/3=13 1/3% учащихся.
(1·13 1/3%)/100%=(40/3)/100=4/30=2/15 часть учащихся на уроке отсутствует.