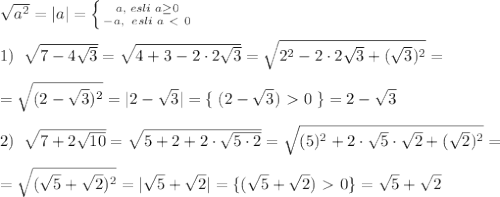
приведу решение другим
составим "дерево вероятности"
по условию "Среди них валиков, изготовленных на первом станке, в 3 раза больше, чем на втором"- значит полная вероятность =1
тогда на 3х(1 станок)+х(второй станок)=1
тогда х= 0,25, 3х=0,75
теперь рисуем "дерево"
валики
1 станок 0,75 2 станок 0,25
высший сорт /не высший сорт высший сорт/ не высший сорт
0,92 / 0,08 0,8 / 0,2
тогда всего валиков высшего сорта 0,75*0,92+0,25*0,8=0,89
валиков высшего сорта с 1 станка 0,75*0,92= 0,69
Тогда выроятность валика высшего сорта с первого станка 0,69/0,89=69/89 ≈0,775
Гипотезы: B₁ - взятый валик с первого станка.
B₂ - взятый валик со второго станка.
Пусть на складе N₁ валиков с первого станка и N₂ валиков со второго станка. Тогда по условию N₁ = 3·N₂.
P(B₁) = N₁/(N₁+N₂) = (3N₂)/(3N₂+N₂) = (3N₂)/(4N₂) = 3/4.
P(B₂) = N₂/(N₁+N₂) = N₂/(3N₂+N₂) = N₂/(4N₂) = 1/4.
Пусть А - событие, что взятый на удачу валик оказался высшего сорта, тогда по формуле полной вероятности:
P(A) = P(A·B₁) + P(A·B₂) = P(B₁)·P(A|B₁) + P(B₂)·P(A|B₂)
По условию P(A|B₁) = 0,92 и P(A|B₂) = 0,8.
P(A) = (3/4)·0,92 + (1/4)·0,8.
P(A·B₁) = P(A)·P(B₁|A).
P(A·B₁) = P(B₁)·P(A|B₁).
P(A)·P(B₁|A) = P(B₁)·P(A|B₁).
По условию необходимо найти P(B₁|A), из последнего равенства имеем
P(B₁|A) = P(B₁)·P(A|B₁)/P(A)
(это формула Байеса)
P(B₁|A) = (3/4)·0,92/((3/4)·0,92 + (1/4)·0,8) =
= 3·0,92/(3·0,92 + 0,8) = 2,76/3,56 = 276/356 = 138/178 = 69/89.
ответ. 69/89.