Пусть х (руб.) покупатель истратил на рынке, тогда в магазине истратил 4х (руб.). Т.к. известна разница, составим уравнение:
4х - х = 1 563
3х = 1 563
х = 1 563 : 3
х = 521 - (руб.) истратил на рынке
521 * 4 = 2 084 руб. - истратил в магазине
521 + 2 084 = 2 605 (руб.) - истратил всего.
Решение не уравнением:
Покупатель потратил 1 часть денег на рынке и 4 части в магазине (в 4 раза больше):
1) 4 - 1 = 3 части - разница ( = 1 563 руб.)
2) 1 563 : 3 = 521 руб. - 1 часть денег
3) 1 + 4 = 5 частей - всего
4) 521 * 5 = 2 605 руб. - истратил всего.
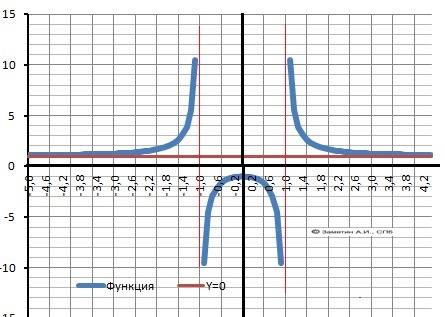
1.Область определения D(x). x²≠1, x ≠ +/-1. - два разрыва.
Х∈(-∞;-1)∪(-1;+1)∪(1;+∞). Две вертикальные асимптоты: х=-1 и х=1.
2. Пересечение с осью Х - нет.
3. Пересечение с осью У. У(0) = -1.
4. Поведение на бесконечности и в точках разрыва.
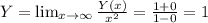
Горизонтальная асимптота - Y=1.
lim(-1-)Y(x)= +∞,lim(-1+)Y(x)= -∞,lim(1-)Y(x)= -∞,lim(1+)= +∞,
5. Исследование на чётность.Y(-x) = Y(x).
Функция чётная.
6. Производная функции.Y'(x).
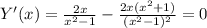
Корень при Х=0.
7. Локальный экстремум - максимум Ymax(0)= - 1.
8. Интервалы возрастания и убывания.
Возрастает - Х∈(-∞;-1)∪(-1;0), убывает = Х∈(0;1)∪ (1;+∞).
8. Вторая производная - Y"(x) = ?.
Корней - нет. Точек перегиба - нет.
9. Выпуклая “горка» Х∈(-1;1), Вогнутая – «ложка» Х∈(-∞;-1)∪ (1;+∞).
10. Наклонная асимптота. Уравнение: lim(oo)(k*x+b – f(x). k=lim(oo)Y(x)/x = 1 - совпадает с горизонтальной.
11. График в приложении.