107+93=200(м/мин)их скорость.
1000:200=5(мин)они встретятся.
150*5=750(м)пробежала обезьяна.
140*5=700(м)пролетел попугай.
ответ:750м;
700м.
Пошаговое объяснение:
1) 20,8
3) 0,00241
5) 2,15
2) 322291
4) 0,025
6) 4
200-1,05+2,62=201,57
y-12,8=0,25
y=13,05
Дано:
S=156,3 км
t(встречи)=3 часа
v(груз.)=65,4 км/час
Найти:
v(велос.)=? км/час
Решение
1) Посчитаем какое расстояние проехал грузовик до встречи с велосипедистом, зная что он ехал 3 часа со скоростью 65,4 км/час:
S(груз.)=v(скорость)×t(время)=65,4×3=196,2 (км)
2) Посчитаем какое расстояние проехал велосипедист за 3 часа, зная что грузовик его догнал через 196,2 км, проехав дополнительно 156,3 км (расстояние между сёлами):
196,2-156,3=39,9 (км)
3) Велосипедист проехал 39,9 км за 3 часа, тогда его скорость равна:
v(велос.)=S÷t=39,9÷3=13,3 (км/час)
ответ: скорость велосипедиста равна 13,3 км/час.
ответ: (e-1)/3
Пошаговое объяснение:
Найдём неопределённый интеграл функции e^(x^3)*x^2 чтобы использовать фундаментальную теорему исчисления.
.
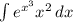Пусть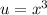 
, тогда ![x=\sqrt[3]{u}](/tpl/images/1117/5039/8c879.png)
.
![du = 3x^2dx \\ dx = \frac{du}{3x^2} = \frac{du}{3(\sqrt[3]{u} )^{2}} = \frac{du}{3u^{2/3}}](/tpl/images/1117/5039/82eee.png)
Делаем подстановку в наше изначальное выражение:
![\int{e^{x^{3}}x^2dx}=\int{e^{u}(\sqrt[3]{u})^{2}\frac{du}{3u^{2/3}} } = \int{ e^uu^{2/3}\frac{du}{3u^{2/3}} }](/tpl/images/1117/5039/640b8.png)
Здесь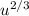 
сокращаются и мы имеем 
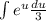. Выносим 
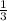за интеграл: 
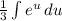. Теперь мы имеем знакомый интеграл, который равняется 
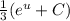, тоже самое что 
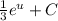. Подставляем 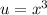и имеем 
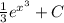. Используем фундаментальную теорему исчисления:
![\int\limits^1_0 {e^{x^3} x^2} = \frac{1}{3} e^{x^3}]_0^1=\frac{1}{3} e^{1^3}-\frac{1}{3} e^{0^3}=\frac{1}{3} e^1-\frac{1}{3} e^0=\frac{1}{3} e-\frac{1}{3}=\frac{e-1}{3}](/tpl/images/1117/5039/3089c.png)
107+93=200м/с - скорость сближения
1000/200=5 минут до встречи
150*5=750м - пробежала обезьянка
140*5=700м - пролетел попугай