190 прямых
Пошаговое объяснение:
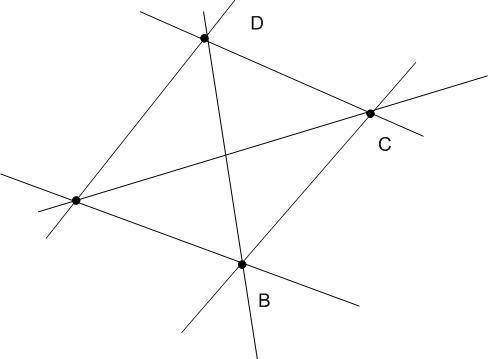
попробуем построить, ну, например для 4-х точек (см.рис).
Прямая проходит через каждые две точки. Т.е. нужно посчитать сколько различных пар точек можно выбрать из 4-х точек. Это - известная в комбинаторике формула для подсчета числа сочетаний (именно сочетаний, а не размещений, потому, что прямая АВ и прямая ВА - одна и таже прямая). Подсчитаем для 4-х точек:
C₄²=4!/(4-2)!4!=4!/(2!*2!)=3*4/2=6;
и действительно видим 6 прямых. Тогда для 20 точек:
C₂₀²=20!/((20-2)!2!)=19*20/2=190.
Пошаговое объяснение:
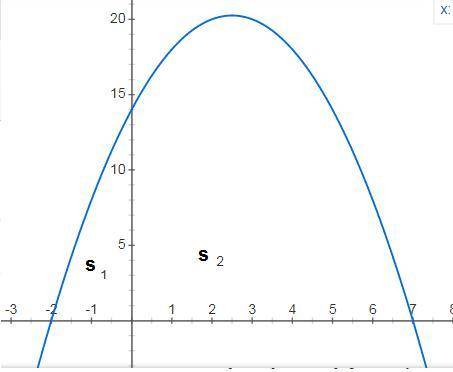
найдем точки пересечения с ОХ
5x+14-x²=0; умножим на -1 ; x²-5x-14=0 ; x₁₋₂=(5±√(25+56)/2=(5±√81)/2=
=(5±9)/2={-2;7}
найдем отдельно площади для х≤0 х≥0 и сложим
₀ ₀
S₁=-∫(5x+14-x^2)dx=-[(5x²/2)+14x-(x³/3)]=-[(5*4/2)-14*2+8/3]=
⁻² ⁻²
=-[10-28+(8/3)]=18-2 2/3=16-2/3=15 1/3
₇ ₇
S₁=∫(5x+14-x^2)dx=[(5x²/2)+14x-(x³/3)]=
⁰ ⁰
=-[(5*49/2)+14*7-342/3]=122,5+98-114=106,5=106 1/2
S=S₁+S₂=15 1/3+106 1/2=121 5/6 кв. единиц
Пошаговое объяснение:
1) Обозначим EF=x MN=x+9
2) Рассмотрим два данных треугольника:
MNP и EFH
1. Угол М = углу F (это дано по условию)
2. Угол N = углу E (это также дано по условию)
Из этих двух пунктов следует, что треугольники MNP и EFH подобны по двум углам( признаки подобия треугольников).
3) Исходя из пункта 2 можно сделать следующую запись: MN/EF=MP/EH=PN/HF. Теперь представим известные по условию задачи величины:
x+9/x=8/3,2=PN/2
4) Разделим данное выражение для удобства счёта:
1. x+9/x=8/3,2
2. 8/3,2=PN/2
Решаем под цифрой 1:
x+9/x=8/3,2
По свойству пропорции:
8•x=3,2(x+9)
8x=3,2x + 28,8
8x - 3,2x = 28,8
4,8x = 28,8
x = 6 отсюда следует, что EF=6, а MN = 6+9=15
Решаем под цифрой 2:
8/3,2=PN/2
По свойству пропорции:
8•2=3,2•PN
PN=8•2/3,2
PN=5
ответ: 6, 15, 5