8
Пошаговое объяснение:
S(ABC)=1/2*AC*BC*sinACB
S(AMC)=1/2*AC*MC*sinACB
S(ABC)/S(AMC)=BC/MC=3
S(AMC)=S(ABC)/3=12/3=4
Рассмотрим △BMK и △AMC. У них <AMC=<BMK как вертикальные, <MAC=<MKB как накрест лежащие. => △BMK ~ △AMC и BM/MC=MK/AM=2:1. Пусть МС=х, тогда ВМ=2х, а если АМ=у, то МК=2у.
Рассмотрим △АМВ и △МКС. Очевидно S(AMB)=S(ABC)-S(AMC)=12-4=8.
При этом S(AMB)=1/2*AM*BM*sinAMB=xy*sinAMB.
S(MKC)=1/2*MK*MC*sinCMK=xy*sinCMK=xy*sinAMB, т.к. <AMB=<CMK как вертикальные.
=>S(MKC)=S(AMB)=8

26 см
Пошаговое объяснение:
Дано:
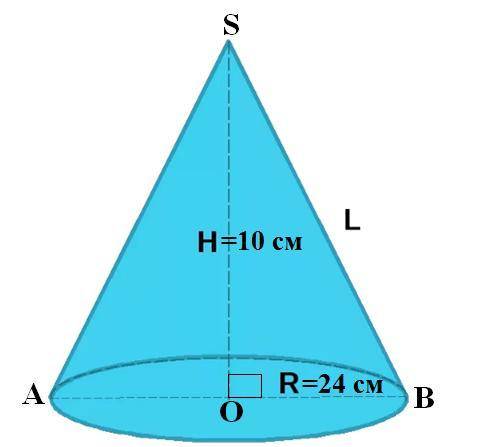
Конус (см. рисунок)
H=10 см - высота конуса
AB=48 см - диаметр основания конуса
Найти: SB - образующую конуса
Решение.
AB=48 см диаметр основания конуса, поэтому радиус основания конуса равен: R=OB=48 см:2=24 см.
Высота конуса это перпендикуляр SO, опущенный из вершины конуса в центр основания. Тогда радиус OB, высота SO и образующая конуса SB образуют прямоугольный треугольник SOB. Для этого треугольник применим теорему Пифагора:
SB²=SO²+OB²= 10²+24²=100+576=676=26².
Отсюда: SB=26 см.