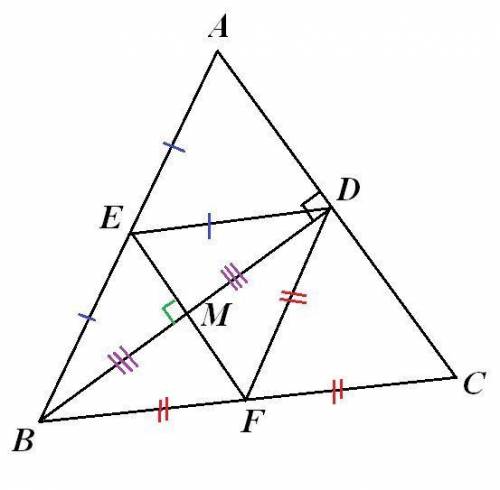
Мой чертеж - во вложении.
1) Докажем сначала пункт Б).
Т.к. по условию Е-середина АВ, F-середина ВС, то EF-средняя линия ΔАВС. ⇒ FE║AC.
Т.к. BD-высота, то BD⊥AC ⇒ BD⊥FE (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и второй прямой). Доказано.
2) Докажем равенство углов EBF и EDF. Пусть BD и EF пересекаются в точке М.
По теореме Фалеса: т.к. FE║AC и F-середина ВС, то М-середина BD.
⇒ в Δ BED EМ-это медиана и высота. ⇒ Δ BED-равнобедренный ⇒ BE=ED.
Аналогично доказывается, что Δ BFD-равнобедренный ⇒ BF=FD.
Рассмотрим Δ EBF и Δ EDF. По доказанному выше они равны по трём сторонам (BE=ED, BF=FD, EF-общая). ⇒∠EBF=∠EDF. Доказано.
Делим 9 монет на 3 части - по 3 монетки. Взвешиваем 3 и 3. Два варианта:
1 вес разный - берем монеты, которые легче, выбираем две и взвешиваем - одна из них легче (фальшивая); одинаковы по массе - третья фальшивая
итого взвешиваний - 2
2 вес одинаков - переходим к третьей кучке монеток. Повторяем предыдущее действие
итого взвешиваний - 2
наименьшее число взвешиваний -2