Стратегия первого: для начала он разбивает 25 камешков на кучки по 1 и по 2. Так, 25=12*2+1, так что он мысленно (или непосредственно раскладывает) разбивает все камешки на 12 пар и 1 камешек. Пусть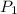 
- это количество групп по одному камешку, а 
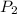- соответственно по два. Назовем разбиение хорошим, если 
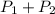нечетно. Если в некоторый момент времени 
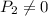, то первый всегда может менять четность суммы 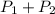, убирая один камешек из групп по одному камешку или два камешка из групп по двое и сохранять ее, убирая один камешек из групп по двое. Если 
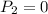и игра еще не окончена, то первый опять мысленно разбивает все камешки на группы по одному и по двое. Стратегия первого будет заключаться в том, чтобы каждый раз после его хода разбиение было хорошим, что, как мы показали, всегда возможно.
сравнить десятичные дроби - значит из большей дроби вычесть меньшую
складывают десятичные дроби так же, как и целые числа по правилам сложения в столбик
умножаем так же, как целые числа, отделяем запятой количество знаков, имеющееся у обеих дробей
делим в столбик, предварительно переносим запятую на нужное количество знаков
(все это есть в учебнике или на сайтах, набери в поисковике, все доступно для понимания)