ответ:
. дан отрезок ав. с циркуля и линейки разделите его на три равные части.
построение. 1) проведем отрезок ав;
2) из точки а проведем окружность произвольного радиуса, которая пересекает отрезок ав в точке д, а его продолжение за точку а - в точке с;
3) из точек с и д проводим окружности радиусом большим сд, пересекающиеся в точках м и n, через полученные точки проводим прямую мn, которая перпендикулярна прямой ав;
4) возьмем произвольную точку р прямой мn и проведем через нее прямую рк, перпендикулярную прямой мn; прямые ав и рк будут параллельны;
5) от начала р луча рм отложим три равных отрезка рр1, р1р2, р2р3, каждый из которых меньше отрезка ав;
6) через точки р3 и в проведем прямую, которая пересечет прямую мn в точке q;
7) проводим прямые р2q и р1q, которые и разделят отрезок ав на три равные части, аа1 = а1а2 = а2в. нетрудно доказать, используя подобие треугольников, что построенные части отрезка ав действительно равны.
пошаговое объяснение:
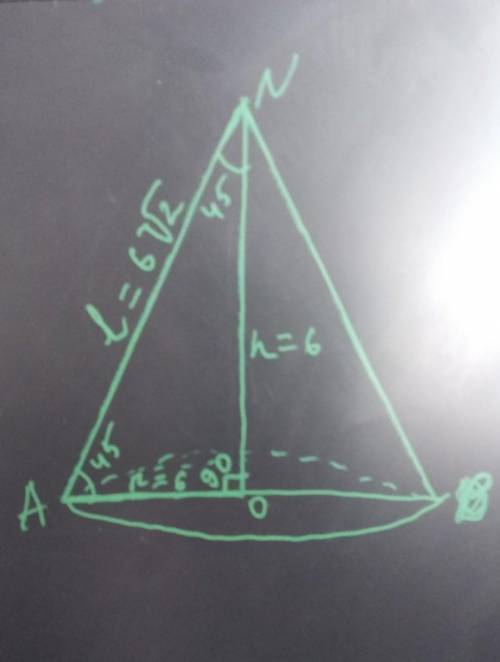
Площадь полной поверхности конуса равна сумме площадей основания конуса и его боковой поверхности:
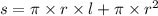
Итак, нам нужно найти:
r - радиус основания
l - длина образующей
Высота известно:
h = 6 см.
Пусть NO высота конуса, AB - диаметр основания (окружности) конуса.
Итак, NO - это высота в равнобедренном прямоугольном треугольном ANB, она также является биссектрисой и медианой этого треугольника. Угол ANO = 90 : 2 = 45'. Это значит треугольник ANO равнобедренный: AO = NO = 45',
h = r = 6. r нашли. По правилу равнобедренного треугольника можно найти и l.
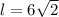
Вот мы нашли r и l. Подставляем в формулу и решим:
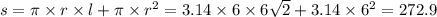
ответ: S = 272.9 см^2