1) Не верно
2) Верно
Понятно???
Пусть скорость автобуса x км/ч, тогда скорость грузовой машины (x+17) км/ч. Скорость сближения x+x+17 = 2x+17 км/ч. Встретились через 3 часа, то есть
(2x+17)\cdot3=453\\2x+17=151\\2x=134\\x=67
Скорость автобуса 67 км/ч, грузовой машины 67+17 = 84 км/ч система уравнений:
Пусть скорость автобуса x км/ч, скорость грузовой машины y км/ч.
Скорость грузовой машины на 17 км/ч больше скорости автобуса, т.е. y-x = 17.
Встретились через 3 часа, то есть (x+y)*3 = 453.
Составим и решим систему уравнений
\begin{cases}y-x=17\\(x+y)\cdot3=453\end{cases}\Rightarrow\begin{cases}x=y-17\\(y-17+y)\cdot3=453\end{cases}(y-17+y)\cdot3=453\\2y-17=151\\2y=168\\y=84\\\begin{cases}x=84-17=67\\y=84\end{cases}
Скорость автобуса 67 км/ч, грузовой машины 84 км/ч.
Пошаговое объяснение:
30 учеников в 6 "а" классе, 24 ученика в 6 "б" классе.
Пошаговое объяснение:Условие задачи (русский):
Количество учащихся в 6 "а" классе на 25% больше, чем количество учащихся в 6 "в" классе. При переводе 3 учащихся из 6 "а" класса в 6 "в" число учащихся в двух классах равнозначно. Сколько учащихся было в каждом классе вначале?
-------------------------------------------------------------------------------------------------------
Пусть
учеников было в 6 "б" классе, тогда в 6 "а" классе было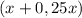 
учеников. В 6 "б" классе стало 
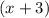учеников после перевода, тогда в 6 "а" классе стало 
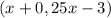учеников. После перевода нескольких учеников, в классах кол-во детей уровнялось. Составим и решим уравнение:
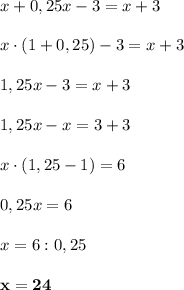
24 ученика было в 6 "б" классе первоначально.
Теперь узнаем кол-во учеников в 6 "а" классе первоначально :
1) 24 + 0,25 · 24 = 24 + 6 = 30 учеников.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Проверка: После перевода нескольких учеников, кол-во детей в классах уровнялось. Проверим это:
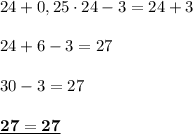
Это значит, что задача решена верно.
1. Не верно
2. Не верно