111, 121, 131, 141, 151, 112, 113, 114, 115, 122, 123, 124, 125, 131, 132, 133, 134, 135, 141, 142, 143, 144, 145, 151, 152, 153, 154, 155. (в сотнях где поставлена цифра "1", также надо заменить на другие имеющиеся в самой задаче цифры)
Пошаговое объяснение:
такие задачи достаточно легкие, если следовать по порядку. сначала в решении изменяем сотни. дальше ставим в десятки любую цифру из задачи, и перебираем единицы. потом сменяем десятки, и также играем с единицами по методу 11, 12, 13, 14, 15, 21, 22, 23, 24, 25 и т. д. когда все возможные варианты с единицами и десятками перепробованы, записываем следующую сотню, и делаем все дальше как по объяснениям выше.
ответ в приложении.
Пошаговое объяснение:
1) Рассмотрим случай, когда у уравнения будет один корень. В этом случае b=3, подставляем в исходное уравнение, получаем, что корнем является 6, но это посторонний корень, значит, корней нет.
2) Рассмотрим случай, когда у уравнения нет корней, то есть дискриминант меньше нуля. Таких значений нет.
3) Рассматривать случай, когда дискриминант больше 0 не имеет смысла, потому что у нас всегда будет два или один (в том случае, когда один из корней посторонний) корней.
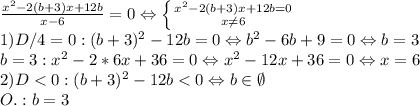
2) х= 2346/23 х=102
3) х= 1190/34 х=35