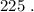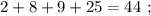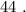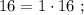
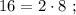
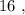 т.е.:
т.е.: 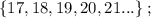
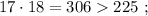
 каждое – будет, очевидно, больше чем
каждое – будет, очевидно, больше чем 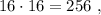 т.е. больше
т.е. больше 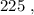 а значит, при выборе минимальных чисел в виде
а значит, при выборе минимальных чисел в виде  и
и  – подобрать остальные числа невозможно.
– подобрать остальные числа невозможно.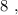 т.е.:
т.е.: 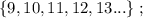
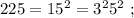
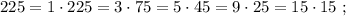
 и
и 
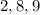 и
и 
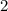 и
и  Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы 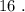
 и
и  никаких натуральных чисел нет.
никаких натуральных чисел нет. и
и 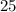 Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы