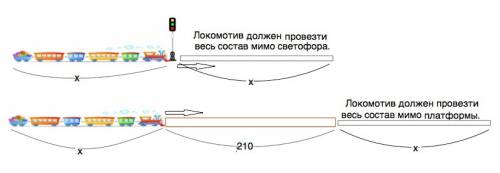
Примем длину поезда за х метров. Тогда мимо светофора он проедет от первого до последнего вагона на расстояние, равное своей длине.( Размерами светофора можно пренебречь, т.к. по сравнению с длиной поезда они чрезвычайно малы).
Скорость вычислим по формуле v=S:t
v=x:5 (м/сек)
Мимо платформы поезд должен проехать расстояние, равное длине платформы плюс всей своей длине, т.е. х+210 метров
Скорость поезда та же:
v=(х+210):20 (м/сек)
Приравняем эти величины:
х:5=(х+210):20
20х=5х+1050
15х=1050
х=70 м - длина поезда.
Принимаем искомую величину, то есть время, через которое автомобили встретятся за х часов. В данной задаче проще производить сравнение по расстоянию. Составим таблицу и найдём «расстояние», которое проехал каждый автомобиль:
Один проехал до места встречи 65х (км), другой 75х (км). По условию расстояние между городами 560 км, значит сумма пройденных расстояний будет равна 560 км. Можем записать:
Автомобили встретятся через 4 часа.
Второй :
Использовать сравнение по времени. Обозначаем расстояние пройденное первым авто как S1, расстояние пройденное вторым авто как S2. Занесем скорость и расстояние в таблицу. Заполняем графу «время»:
Известно, что ехали они одинаковое время (с момента выезда каждого из своего пункта и до момента встречи). Так же известно, что сумма расстояний пройденных ими равна 560 км.
Можем составить два уравнения и решить систему:
Решив её, получим S1=260 км и S2=300 км.
Найдём время:
*Первый более рационален, решение сводится к линейному уравнению.
ответ: 4



пусть меньший угол(2) =x,тогда больший угол(1)=x+20
составляем и решаем уравнение
x+x+20=180 т.к. сумма углов =180градусов
2x=180-20
x=160/2
x=80 градусов меньший угол 2)больший угол =80+20=100градусов