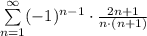
Исследуем этот ряд на абсолютную сходимость.
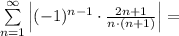
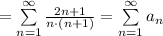
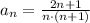
Рассмотрим ряд
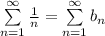
Используем предельный признак сравнения:
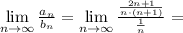
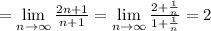
Значит ряды 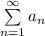 и
и 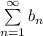
сходятся или расходятся одновременно, но ряд
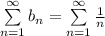
это гармонический ряд, который расходится. Значит и ряд
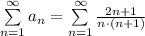
расходится.
Исследуем данный в задании ряд на условную сходимость. Используем признак Лейбница. Ряд знакочередующийся.
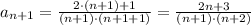
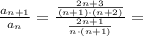
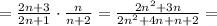
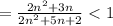
т.к. 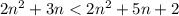 ⇔
⇔ 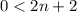 ⇔
⇔ 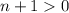 .
.
То есть 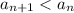 .
.
То есть последовательность 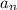 монотонно убвывает.
монотонно убвывает.
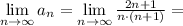
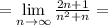
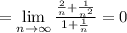
То есть последовательность 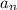 монотонно убвывает и стремится к нулю. Итак, по признаку Лейбница, исходный ряд сходится.
монотонно убвывает и стремится к нулю. Итак, по признаку Лейбница, исходный ряд сходится.
ответ. Сходится условно.
1) (-2,5+2 1//3)*(-5 1//7)+1 1//3:(-5,6)=(-2.5+(7//3))*(-(5 1//7))+(1 1//3):(-5.6)=(-(1//6))*(-(5 1//7))+(1 1//3):(-5.6)=(-(1//6))*(-(36//7))+(1 1//3):(-5.6)=-(1//6)*(-(36//7))+(1 1//3):(-5.6)=-(-(1//6)*(36//7))+(1 1//3):(-5.6)=-(-(6//7))+(1 1//3):(-5.6)=(6//7)+(1 1//3):(-5.6)=(6//7)+(4//3):(-5.6)=(6//7)+(-(4//3)/5.6)=(6//7)+(-(5//21))=(6//7)-(5//21)=13//21 (0.619047619047619)
2)15,87*(-1,09)+(-5,87)*(-1,09) = -1,09 * (15,87 - 5,87) = -1,09 * 10 = -10,9
3) а) 0,(7) = 7//9
в) 2,3(72) =2(372-3//990)=2369//990=2123//330
4)S=22.4км
V=14,5 скорость велосипедиста
t=2//3ч
V=? мотоциклиста
решение.
14,5км/ч*2//3ч=(145*2)//10*3=9,6 км(Vвелосипедиста за 2//3ч)
22,4км +9,6км=32км (проехать мотоциклисту)
32:2//3=48 км/ч
ответ: 48 км/ч
Пошаговое объяснение:
// - знак дроби
в3-ем задании в)2- это целое, пиши между дробями в начале
2)(684+915)-484=(684-484)+915=200+915=1115
3)(259+101)-59=(259-59)+101=200+101=301
4)1287-(487+164)=(1287-487)+164=800+164=964
5)971-(235+371)=(971+371)-235=1107
6)5393-(1393+158)=(5393-1393)+158=4000+158=4158