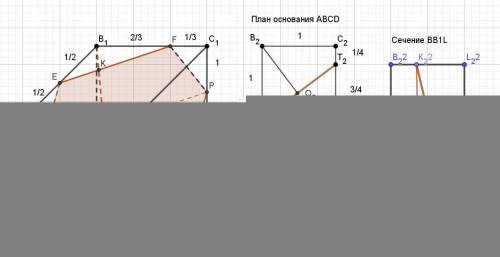
А) Построено сечение прямоугольного параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей середины рёбер A1B1, CC1, и вершину А (вложение 1).
Заданы точки А,Е и Р. За основу построения сечения принято свойство - в параллельных плоскостях линии сечения параллельны.
Проводим первый отрезок АЕ. В плоскости грани АА1В1В он проходит под углом к АА1, тангенс которого равен (1/2)/2 = 1/4. Под таким же углом к ребру СС1 проводим отрезок РТ. Точка Т разделит ребро CD основания на расстоянии (1/4) от точки С. Отрезок DT равен 1 – (1/4) = (3/4).
Далее проводим АТ по полученным точкам на основании АВСD и параллельно проводим под углом, тангенс которого равен (3/4) отрезок EF на верхнем основании. Этим определяется положение точки F, которая на ребре В1С1 выделит в отношении (1/2) / (3/4) = 4/6 = 2/3 отрезок B1F.
Отрезок FC1 = 1 – (2/3) = 1/3.
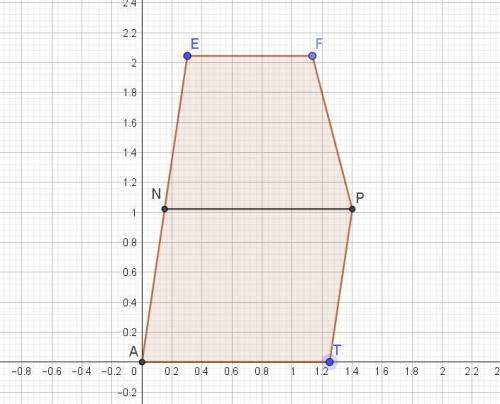
Б) Найдена площадь полученного сечения, из условия: ABCD-квадрат со стороной 1, а AA1=2 (вложение 2). Сечение дано в натуральную величину.
Оно разбито линией NP, параллельной АТ на 2 фигуры - трапецию и параллелограмм.
Положение точек Р и Т определено из подобия треугольников.
Так как точка Р находится на середине ребра СС1, то высоты трапеции и параллелограмма равны.
Длины оснований определяем по Пифагору.
АТ = √(1² + (3/4)²) = √(1 + (9/16)) = 5/4 = 1,25.
EF = √((1/2)² + (2/3)²) = √((1/4) + (4/9)) = √(9 + 16)/9) = 5/6.
Определяем наклонную высоту сечения. Для этого проводим секущую плоскость BB1L, перпендикулярную плоскости сечения.
Находим косинус угла D1FE: cos(D1FE) = (2/3) / (5/6) = 4/5, затем синус: sin(D1FE) = √(1 – (4/5)2) = 3/5.
Отсюда В1К = (2/3)*(3/5) = 2/5 = 0,4. Аналогично находим LQ = (3/4)*(3/5) = 9/20 = 0,45.
Отрезок BL = AT = 1,25, тогда проекция KQ на основание равна 1,25 – 0,4 – 0,45 = 0,4.
Наклонная высота сечения равна KQ = √(2² + 0,4²) = √4,16 ≈ 2,04.
Высоты частей сечения (трапеции и параллелограмма) равны по 2,04/2 = 1,02.
Находим площади трапеции S1 и параллелограмма S2 при условии NP = AT = 1,25.
S1 = ((EF + NP)/2)*1,02 = ((5/6)+1,25)/2)*1,02 = 1,041667*1,02 = 1,0625.
S2 = AT*1,02 = 1,25*1,02 = 1,275.
S = 1,0625 + 1,275 = 2,3375 кв.ед.
Числитель: (1,75 · 3 2/3 + 1/3 · 1,75) : 0,1 · 4/7 - 21 1/3 = 18 2/3
1) Общий множитель 1,75 выносим за скобки:
= 1,75 · (3 2/3 + 1/3) = 1,75 · 4 = 7
2) 7 : 0,1 = 70
3) 70 · 4/7 = 10 · 4 = 40
4) 40 - 21 1/3 = 39 3/3 - 21 1/3 = 18 2/3
- - - - - - - - - - - - - - -
Знаменатель: 0,4 · 4 5/6 · 2,5 - 9 : (5 4/5 · 0,1 + 1,42) = 1/3
1) (0,4 · 2,5) · 4 5/6 = 1 · 4 5/6 = 4 5/6
2) 5 4/5 · 0,1 = 5,8 · 0,1 = 0,58
3) 0,58 + 1,42 = 2
4) 9 : 2 = 9/2 = 4 1/2
5) 4 5/6 - 4 1/2 = 4 5/6 - 4 3/6 = 2/6 = 1/3
- - - - - - - - - - - - - - -
Числитель/Знаменатель: 18 2/3 : 1/3 = 56/3 · 3/1 = 56
- - - - - - - - - - - - - - -
Пропорция: 56 - 100%
х - 75%
х = 56 · 75 : 100 = 42
Или так: 56 · 0,75 = 42
ответ: 42.
Здесь есть ответ и написано что одно равно другому! Все верно сделано зато!