1) положительное число всегда больше отрицательного;
2) ноль меньше положительного числа, но больше отрицательного;
3) при сравнении двух отрицательных чисел, меньше то число, чей модуль больше;
4) при сравнении десятичных дробей сравниваем целые части - больше то число, у которого больше целое; если целые равны - сравниваем десятичные и т.д.;
5) при сравнении обыкновенных дробей с одинаковым числителем больше та дробь, у которой меньше знаменатель;
6) при сравнении обыкновенных дробей с одинаковым знаменателем больше та дробь, у которой больше числитель.
1) 135 > - 136
2) - 74 < 0
3) - 3,4 > - 3,8
4) - 0,2000 > - 0,2001
5) - 7/13 < - 7/16
1) - 58 < 43
2) 0 > - 35
3) - 92 < - 89
4) - 1,100 < - 1,099
5) - 5/7 < - 9/14, (т.к. - 5/7 = - 10/14, а - 10/14 < - 9/14)
в порядке убывания:
9,5 > 8,9 > 7 > 0 > - 4,8 > - 4,9 > - 10,9
в порядке возрастания:
- 11 < - 6 < - 5,9 < 0 < 0,5 < 4,5 < 5,3
Пошаговое объяснение:
2. Рассм. ΔСОВ и ΔВОА
СО=ВО=АО=R
∠CОВ=∠ВОА
⇒ ΔСОВ=ΔВОА (по 1 признаку) ⇒АВ=ВС
4. Рассм. ΔСОВ
ОВ=ОС=R ⇒ΔСОВ - равнобедренный ⇒ ∠1=∠С
∠2=∠1+∠С (внешний) ⇒ ∠2=2∠1
6.
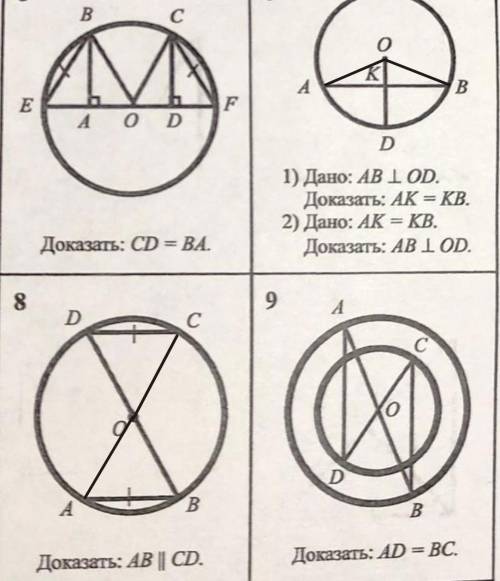
1) Рассм. ΔАОК и ΔКОВ - прямоугольные
АО=ОВ=R
ОК - общая ⇒ ΔAOK=ΔKОB (по катету и гипотенузе)
⇒ АК=КВ
2)Рассм. ΔАОК и ΔКОВ
АО=ОВ=R, АК=КВ (усл)
ОК - общая ⇒ ΔAOK=ΔKОB (по 3 признаку)
⇒∠АКО=∠ОКВ=180°:2=90° (смежные) ⇒ АВ⊥ОD
8.Рассм. ΔODC и ΔAOB
OD=OC=OA=OB=R
DC=AB (усл)
⇒ ΔODC=ΔAOB (по 3 признаку)
⇒∠D=∠B - накрест лежащие при AB и DC и сек.DB ⇒ AB||DC
HOK=(a*b)/НОД
НОК=1440/18=80