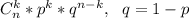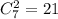 выбрать одно элементарное событие из 6^7 возможных, так, чтобы пятерка выпала только в двух испытаниях. Вероятность каждого из таких событий - это произведение вероятностей двукратного выпадения 5 и пятикратного выпадения не 5, то есть
выбрать одно элементарное событие из 6^7 возможных, так, чтобы пятерка выпала только в двух испытаниях. Вероятность каждого из таких событий - это произведение вероятностей двукратного выпадения 5 и пятикратного выпадения не 5, то есть 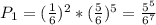 . Умножая на число событий, получаем, что вероятность искомого события равна
. Умножая на число событий, получаем, что вероятность искомого события равна 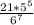 , или приблизительно 23,44%
, или приблизительно 23,44%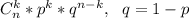
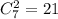 выбрать одно элементарное событие из 6^7 возможных, так, чтобы пятерка выпала только в двух испытаниях. Вероятность каждого из таких событий - это произведение вероятностей двукратного выпадения 5 и пятикратного выпадения не 5, то есть
выбрать одно элементарное событие из 6^7 возможных, так, чтобы пятерка выпала только в двух испытаниях. Вероятность каждого из таких событий - это произведение вероятностей двукратного выпадения 5 и пятикратного выпадения не 5, то есть 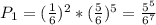 . Умножая на число событий, получаем, что вероятность искомого события равна
. Умножая на число событий, получаем, что вероятность искомого события равна 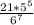 , или приблизительно 23,44%
, или приблизительно 23,44%