площадь квадрата находится по следующей формуле
S=a²
а-это сторона квадрата.
1).а)если сторону увеличить в 2 раза, то она будет равна 2а, тогда площадь будет находиться по формуле
S=(2a)²=4а²
теперь вычислим разницу
4а²:a²=4(т.е. а² сокращается)
ответ: в 4 раза
б)если сторону увеличить в 3раза, то она будет равна 3а, тогда площадь будет находиться по формуле
S=(3a)²=9а²
теперь вычислим разницу
9а²:a²=9(т.е. а² сокращается)
ответ: в 9 раз
2) 9*74=666
теперь увеличим первый множитель(т.е.9) на 8. 9+8=17
умножим полученное число на 74
17*74=1258
теперь вычтем из 1258 666
1258-666=592
ответ:значение произведения увеличится на 592.
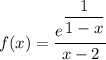1. Рассмотрим точку 11. Тут явно разрыв, так как функция не определена
2. Вычислим односторонние пределы
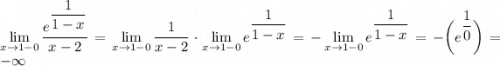
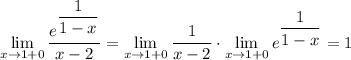
То есть функция сначала ушла в -∞ а затем резко появилась в 1
это разрыв второго рода
2. Рассмотрим точку 21. Тут опять разрыв, смотрим какой
2. Вычислим односторонние пределы
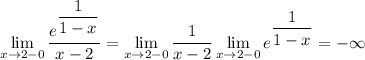
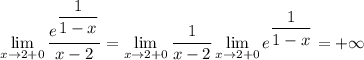
То есть функция сначала уходит в -∞ а потом выходит из +∞
В этой точке тоже разрыв второго рода
