Пошаговое объяснение:
Вспоминаем свойства степеней, это алгебра 7-го класса. Фото внизу.
Задача 497.
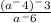
В этом примере необходимо раскрыть скобки. Св-во степени: при раскрытии скобок показатели степеней перемножаются.
Получаем:
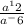
При делении показатели степеней вычитаются!
Получаем:
a^12 - (-6) = a^12+6 = a^18 (^ - степень).
Задача №498. (Попробуй решить самостоятельно).
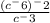
Тут опять же раскрытие скобок и деление. (Свойства при раскрытии скобок и делении выше!).
Получаем: c^12-(-3) = c^15 (^ - степень!)
Задача 499.
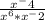
Тут для начала надо разобраться с знаменателем дроби: при умножении степени складываются.
Получаем:
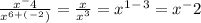
Задача 500.
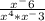
Производим манипуляции со степенями в знаменателе(степени при умножении складываются) и получаем:
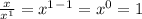
И вот тут еще одно свойство степеней: число, которое возводят в нулевую степень, будет всегда равно единице.
Задача 501.
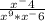
И опять мы делаем свои дела в знаменателе, получаем дробь:
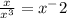
Задача 502.
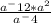
Делаем свои дела уже в числителе. Получим дробь:
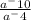 = a^-6
= a^-6
Не забудь, что при делении степени вычитаются!

Начнём вот с какого факта: пусть a>1; положим a=1+α. Тогда an=(1+α)n=1+nα+n(n−1)2α2+⋯, где все остальные члены неотрицательны. Отсюда следует, что экспонента растёт быстрее квадратичной функции (коэффициент при n2 здесь положителен). Понятно, что такая квадратичная функция растёт быстрее линейной.
Это рассуждение доказывает, что limn→∞nan=0 при a>1. То же самое можно записать в виде n=o(an), где n→∞. Отсюда легко распространить утверждение на случай функций вместо последовательностей: limx→+∞xax=0, или x=o(ax) при x→+∞.
Блин слушай я так решала
315-148+185=167+185=352
при р=213
315-213+185=102+185=287