0,6
Пошаговое объяснение:
Количество двузначных чисел от 10 до 99 составляет 90.
Числа, которые делятся на 2, это числа которые оканчиваются цифрами 0, 2, 4, 6 или 8.
Числа, которые делятся на 5, это числа которые оканчиваются цифрой 0 или 5.
Числа, которые делятся на 2 и 5, это числа которые оканчиваются цифрой 0.
Таким образом, среди каждого десятка двузначных чисел количество чисел, которые подходят под критерии, а именно оканчиваются на одну из цифр 0, 2, 4, 5, 6, 8, составляет 6 штук. Например, в десятке чисел от 30 до 39, на 2 делятся 30, 32, 34, 36, 38, а на 5 делится 35, и на 2 и 5 делится 30, то есть подходящие под нужный критерий числа - это числа 30, 32, 34, 35, 36, 38, всего 6 штук.
Так как всего двузначных чисел 90, то есть 9 десятков, то подходящих чисел будет 9*6 = 54.
По классическому определению вероятности, вероятность того , что наудачу взятое двухзначное число окажется кратным либо 2, либо 5, либо тому и другому одновременно составляет 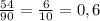
0,6
Пошаговое объяснение:
Количество двузначных чисел от 10 до 99 составляет 90.
Числа, которые делятся на 2, это числа которые оканчиваются цифрами 0, 2, 4, 6 или 8.
Числа, которые делятся на 5, это числа которые оканчиваются цифрой 0 или 5.
Числа, которые делятся на 2 и 5, это числа которые оканчиваются цифрой 0.
Таким образом, среди каждого десятка двузначных чисел количество чисел, которые подходят под критерии, а именно оканчиваются на одну из цифр 0, 2, 4, 5, 6, 8, составляет 6 штук. Например, в десятке чисел от 30 до 39, на 2 делятся 30, 32, 34, 36, 38, а на 5 делится 35, и на 2 и 5 делится 30, то есть подходящие под нужный критерий числа - это числа 30, 32, 34, 35, 36, 38, всего 6 штук.
Так как всего двузначных чисел 90, то есть 9 десятков, то подходящих чисел будет 9*6 = 54.
По классическому определению вероятности, вероятность того , что наудачу взятое двухзначное число окажется кратным либо 2, либо 5, либо тому и другому одновременно составляет 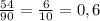
По признаку делимости на 5, наше число оканчивается на 5 или 0. По признаку делимости на 8, три последние цифры нашего числа делятся на 8. По признаку делимости на 9, сумма цифр нашего числа делится на 9.
Число 1993 даёт остаток 4 от деления на 9, следовательно, нужно добавить к числу несколько цифр, сумма которых даёт остаток 5 от деления на 9. При этом полученное число будет оканчиваться на 0. Переберём возможные варианты (от меньшего к большему):
Добавим две цифры (одну нельзя, так как нужен "0" и ещё что-то):
199350 не делится на 8.
С двумя не получилось, попробуем три:
1993050 не делится на 8.
1993140 не делится на 8.
1993230 не делится на 8.
1993320 : 2520 = 791.
Значит, требуемое число - 1993320, так как оно делится на НОК чисел от 1 до 9.
ответ: 1993320.