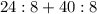
повторяется, поэтому вынесем это действие за скобку. Получим такое числовое выражение:
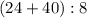
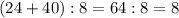В ответе у нас получилось целое число. Значит можно считать утверждение "если каждое из двух чисел делится на , то и их сумма делится на .
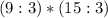
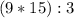
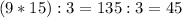
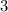,то их произведение делится на 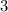" доказанным.
Начнём вот с какого факта: пусть a>1; положим a=1+α. Тогда an=(1+α)n=1+nα+n(n−1)2α2+⋯, где все остальные члены неотрицательны. Отсюда следует, что экспонента растёт быстрее квадратичной функции (коэффициент при n2 здесь положителен). Понятно, что такая квадратичная функция растёт быстрее линейной.
Это рассуждение доказывает, что limn→∞nan=0 при a>1. То же самое можно записать в виде n=o(an), где n→∞. Отсюда легко распространить утверждение на случай функций вместо последовательностей: limx→+∞xax=0, или x=o(ax) при x→+∞.
Блин слушай я так решала
Получится 24 случая. Кароче у тебя 2 супа 3 блюда и 4 компота. Для того чтобы узнать сколько случаев будет тебе надо умножить 2*3*4=24 случая.