ответ: Пустое множество!
Пошаговое объяснение:
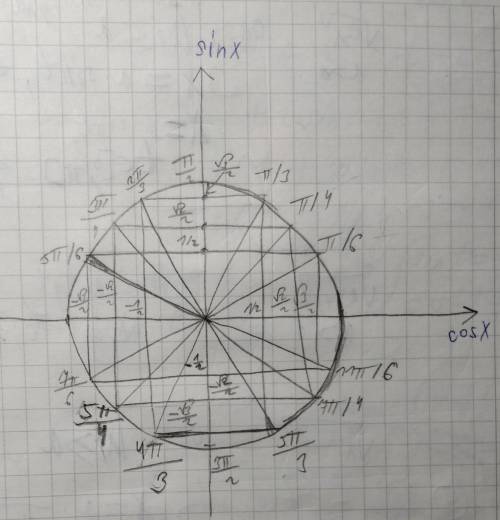
Графически (а в более сложных случаях и методом интервалов, но не в данной задаче) неравенства с тригонометрическими функциями решать как по мне наиболее удобный вариант – нужно только знать какие значения и где на окружности, если что я прикрепила свой может неаккуратный, но применимый для решения рисунок со значениями. Если что, синус угла x – ордината точки, что получена поворотом точки с координатами 1;0 вокруг начала координат на направленный угол x (направленный угол значит двигается против часовой стрелки положительный угол и по угол со знаком –)
А косинус угла х абсцисса точки, полученная аналогичным образом.
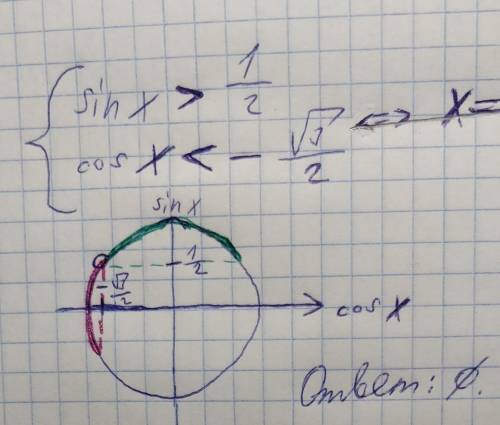
В этой задаче рисуем и получается, что единственное возможное пересечение (а так как у нас система, это и будет решением) – значение угла, чей синус равен 1/2, а косинус –√3/2, НО так как тут в системе строгие неравенства, то ответом является пустое множество.
Пошаговое объяснение:
1) найдем критические точки
f'(x) = (x²/4)' +(2x)' +(7)' = x/2 - 2 ⇒ на [0;3] f'(x)≠0
критических точек нет
ищем значение функции на концах отрезка
х =0; f(x) = 7 - максимум
х=3; у = 13/4 - минимум
2) квадрат диагонали боковой грани д₁ = 2² + 5² = 29
теперь из треугольника, образованного диагональю грани, диагональю параллелепипеда и третьим ребром параллелепипеда найдем нужную диагональ
д₂² = 29+35 = 64
д₂ = 8
3) образующая конуса и радиус цилиндра образуют прямоугольный треугольник
высота цилиндра:
h² = 10² - 8² = 36
h = 6