63.
Пошаговое объяснение:
Рассмотрим все пары натуральных чисел, удовлетворяющих условию m+n=16:
1) 1 и 15 взаимно простые, произведение 1•15 = 15;
2) 2 и 14 не являются взаимно простыми, (например, имеют общий делитель 2);
3) 3 и 13 взаимно простые, произведение 3•13 = 39;
4) 4 и 12 не являются взаимно простыми, (например, имеют общий делитель 2);
5) 5 и 11 являются взаимно простыми, произведение 5•11 = 55;
6) 6 и 10 не являются взаимно простыми, (например, имеют общий делитель 2);
7) 7 и 9 являются взаимно простыми, произведение 7•9= 63;
8) Пара 8 и 8 не удовлетворяет условию, слагаемые не являются взаимно простыми, (например, имеют общий делитель 2)
Остальные пары чисел будут отличаться лишь порядком следования и были рассмотрены.
Наибольшее произведение слагаемых 7 и 9 равно 7•9= 63.
№1
-1,2 * (-15) = (-1 * 1,2) * (-1 * 15) = (-1 * (-1)) * (1,2 * 15) = 1 * 18 = 18
-1,95 - 8,68 = -1 * (1,95 + 8,68) = 10,63
-17 - 19 + 5 = -1 * (17 + 19 - 5) = -21
-13,5 : 0,9 = -1 * (13,5 : 9/10) = -1 * (13,5 * 10 : 9) = -1 * (15) = -15
№2
-15 -14 -13 -12 ... -1 0 1 ... 15 16
Если посчитать будет 15 отрицательных, 1 ноль и 16 положительных. Итого 15 + 1 + 16 = 32 числа
№3
3(4x + 5) - (21 + 12x) = 12x + 15 - (21 + 12x) = 12x + 5 - 21 - 12x = 0 + 5 - 21 = -1 * (21 - 5) = -16
№4
4x - 2,55 = -2x + 1,05
4x + 2x = 2,55 + 1,05
6x = 3,6
x = 0,6
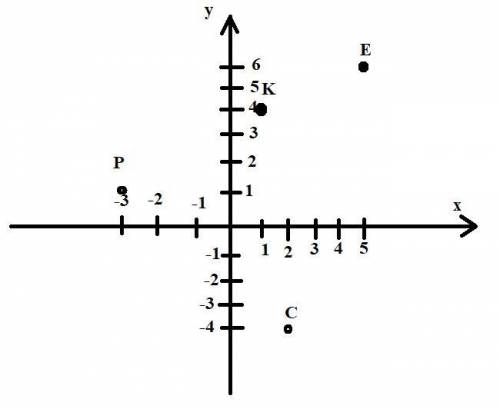
№5
Прикрепленный файл.
Пошаговое объяснение: