5
⊂_ヽ
＼＼ ___
＼( •_•)
< ⌒ヽ
/ へ＼
/ / ＼＼
ﾚ ノ ヽ_つ
/ /
/ /|
( (ヽ
| |、＼
| 丿 ＼ ⌒)
| | ) /
`ノ ) Lﾉ
.,,..;~` `＜``彡 }
_...:=,`' ︵ т ︵ X彡-J
＜` 彡 / ミ ,_人_. ＊彡 `~
`~=:: Y
i. .:
.\ ,｡---.,, ./
ヽ ／ﾞ''```\;.{ ＼／
Y `J..r_.彳 |
{ `` ` i
\ ＼ ..︵︵.
`＼ ``ゞ.,/` oQ o`)
`i, Y ω /
`i, . » /
`iミ ,,ノ
︵Y..︵.,, ,,+..__ノ``
(,`, З о ,.ノ川彡ゞ彡 ＊
Для начала поработаем со вторым выражением. Первые три слагаемых свернем в квадрат разности: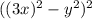
; В следующих двух слагаемых вынесем общий множитель "40": 
; В итоге получим следующее уравнение: 
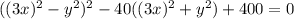. В скобках мы видим похожие выражения, отличающиеся лишь знаком посередине (такие выражение называются сопряженными). А хотелось бы видеть там равные (строго говоря тождественные) выражения. Пусть в первой скобке вместо 
будет стоять 
; Это приведет к тому, что придется убавить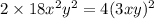 
; В итоге: 
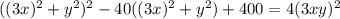; Слева стоит квадрат суммы. Уравнение примет вид: 
; Сворачивая еще раз: 
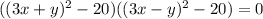; Получаем серию прямых: 
; А теперь приступим к рассмотрению первого уравнения.
Это уравнение задает круг с центром в точке (0, 0) и радиусом
; Рассмотрим прямую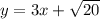 
; Найдем радиус окружности с центром в начале координат, которая касается данной прямой. Это легко сделать из подобия треугольников. 
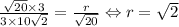; Значит, круг касается всех этих четырех прямых. Достаточно найти только координаты касания с любой из прямых. Это делается так же, как и находился радиус окружности. Для той же прямой это координаты 
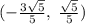; Ну а все решения: