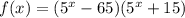
Уравнение касательной имеет вид:
 ,
,
где 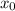 — абсцисса точки графика функции
— абсцисса точки графика функции 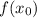 , к которому проведена касательная
, к которому проведена касательная 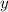 .
.
Так как график касательной имеет вид график прямой линейной функции 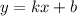 , а по условию она должна быть горизонтальной, значит, это частый случай линейной функции —
, а по условию она должна быть горизонтальной, значит, это частый случай линейной функции — 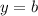
Таким образом, касательная будет горизонтальной, если 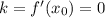
Найдем 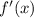 :
:
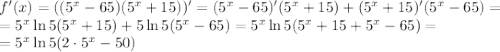
Найдем 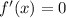 :
:
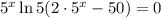

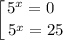
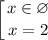
Следовательно, 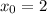 — абсцисса точки графика функции
— абсцисса точки графика функции 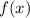 , к которому проведена касательная
, к которому проведена касательная 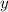 .
.
Найдем значение 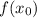 :
:
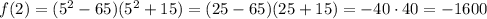
Таким образом, 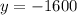 — уравнение горизонтальной касательной к графику функции
— уравнение горизонтальной касательной к графику функции 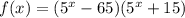
ответ: 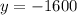
1)первое число х, второе у.
х-у=135
х/у=4 остаток 12
чтобы найти делимое, надо делитель умножить на частное и прибавить остаток.
х=4у+12
решаем систему
х-у=135
х=4у+12
подставляем значение х в первое уравнение
4у+12-у=135
3у=123
у=41, х=4*41+12=176.
это числа 176 и 41.
2) дорога из школы домой занимает у вики на 5 мин больше.отнимем эти 5 мин от общего времени. 37-5=32. это время она одинаково тратит на дорогу туда и обратно, т.е. по 32/2=16 мин. но на дорогу домой еще плюс 5 мин . 16+5=21.
таким образом в школу она идет 16 мин, а домой 21 мин.
3) первое число х, второе у.
х+у=2,5х
у-х=4,5
у=1,5х
у-х=4,5
1,5х-х=4,5
0,5х=4,5
х=9; у=1,5*9=13,5
это числа 9 и 13,5.
4) есть сумма трёх чисел. первое х. тогда второе 2,5х, а третье 3,5х. их сумма 10,5.
х+2,5х+3,5х=10,5
7х=10,5
х=1,5
первое число 1,5. второе 2,5*1,5=3,75. третье 1,5*3,5=5,25.
5) аналогично. числа х и у. система.
х+у=12 х=12-у
х*у=35 х*у=35
у(12-у)=35
12у- =35
=35
D=b 2 - 4ac = 4
√D = 2
у 1 = -b + √D = 12 + 2 = 7 2a 2 × (1 )у 2 = -b - √D = 12 - 2 = 5 2a 2 × (1 )
есть два решения: у=7, х=12-7=5 и у=5, х=12-5=7.
6) первое число х, второе х+250. их сумма -130
х+х+250=-130
2х=-380
х=-190
первое число -190, второе -190+250=60.
7) первая дробь х, вторая х-13,2. их сумма 8,4.
х+х-13,2=8,4
2х=21,6
х=10,8
первая дробь 10,8. вторая 10,8-13,2=-2,4.
8) во втором цехе х рабочих. в первом 1,2х рабочих. в третьем х+200. всего 1800 чел.
х+1,2х+х+200=1800
3,2х=1600
х=500
во втором цехе 500 рабочих. в первом 1,2*500=600 рабочих. в третьем 500+200=700 рабочих.
9) пете х лет. васе 1,5х лет. коле 1,5х+4 лет. всем вместе 36 лет.
х+1,5х+1,5х+4=36
4х=32
х=8
пете 8 лет. васе 1,5*8=12 лет. коле 12+4=16 лет.
10) х+у=56
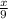 =
= 
чтоб избавиться от дроби, перемножим во втором уравнении делимые на противоположные делители
5х=9у, решаем систему
х+у=56
5х=9у
х=56-у
5х=9у подставляем значение х во ворое уравнение
5(56-у)=9у
280-5у=9у
14у=280
у=20; х=56-20=36.
20+36=56
Думаю из этого вы сможете составить реферат:
В результате развития человеческого общества появилась необходимость в измерении длины, площади, веса и т. д. В этом деле не обойтись одними целыми числами, люди ввели дроби.
Вначале это были так называемые «обыкновенные дроби». Главное их неудобство состояло в том, что долями единицы (знаменателями) могли быть любые числа. И в процессе счета нужно было приводить дроби к одному знаменателю. Тогда появилась: идея создания систематических дробей, в которых единица всегда имеет одинаковое число долей.
Самые первые систематические дроби появились в Вавилоне за 2 тысячи лет до нашей эры. В них единица делилась на шестьдесят долей, так как «круглым» числом у вавилонян считалось не 10, а 60. Вавилонские дроби, в отличие от всей шестидесятеричной системы счета, были заимствованы древними греками, а от них и европейцами. Этой системой пользовались в Западной Европе, в основном астрономы, до конца XVI века.
В Древнем Риме существовала двенадцатеричная система дробей (единица делилась на двенадцать долей). Это было связано с тем, что денежная единица древних римлян (она же единица веса) асc делилась на двенадцать унций. Унцией называли не только мелкую монету, но и вообще дробь, которую мы называем «одна двенадцатая», даже если она употреблялась для измерения длины.
Наши обыкновенные дроби широко употреблялись древними греками и индийцами. Правила действий с дробями, изложенные индийским ученым Брамагуптой, в IX веке распространились в мусульманских странах благодаря Мухаммеду Хорезмскому. В Западную Европу их привез итальянский купец и ученый Леонардо Фибоначчи из Пизы в XIII веке.
Наконец, выдающийся самаркандский математик Гиясэддин Джемшид ал-Каши (XIV-XV века) ввел десятичные дроби, которыми мы пользуемся и сейчас. Когда в XVI веке голландский купец и инженер Симон Стевин познакомил с ними Европу, они полностью вытеснили громоздкие шестидесятеричные дроби.
В первых учебниках дроби назывались “ломаные числа”. Современное обозначение дробей берёт своё начало в Древней Индии. В начале в записи дробей не использовалась дробная черта. В русском языке это слово появилось в XVIII веке, оно происходит от глагола “дробить” - разбивать, ломать на части.
Народы через многие варианты записи дробей, пока не пришли к современной записи.
Вначале в записи дробей не использовалась дробная черта, например число записывалось так .
Черта дроби появилась лишь только в 1202 году у итальянского математика Леонардо Пизанского. Он ввел слово дробь. Названия числитель и знаменатель ввел в 13 веке Максим Плануд - греческий монах, ученый, математик.
Современную систему записи дробей создали в Индии. Только там писали знаменатель сверху, а числитель снизу, и не писали дробной черты. А записывать дроби как сейчас стали арабы.