Пошаговое объяснение:
а) 4,8,12,16…;
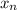 =4n
=4n
б) 1,-1,1,-1….
 =
=
2. Последовательность задана в аналитической форме yn=2n+10
Найти 10,50,63 член последовательности.
y₁₀=2·10+10=30
y₅₀=2·50+10=110
y₆₃=2·63+10=136
3. Последовательность задана в аналитической форме yn=n² +2.
Найти 5,10,13 член последовательности.
y₅=5²+2=25+2=27
y₁₀=10²+2=102
y₁₃=13²+2=171
4. Последовательность задана в рекурсивном виде y1=5
y n =y n-1 −3 , если n=2,3,4…
Найти 5,11,12 член последовательности.
y₅=y₄-3=y₃-3-3=y₂-3-3-3=y₁-3-3-3-3=y₁-4·3=5-4·3=-7
y₁₁=y₁₀-3=...=y₁-(11-1)·3=5-10·3=-25
y₁₂=y₁₁-3=...=y₁-(12-1)·3=5-11·3=-28
Это арифметическая прогрессия с разностью -3. Несложно доказать преобразуя данное рекурсивное соотношение
5. Последовательность задана в рекурсивном виде y 1 =3, y 2 =8 , y n =2y n-2 +3,
если n=3,4,5…. Найти 3,4,9 член последовательности.
y₃=2y₁+3=2·3+3=9
y₄=2y₂+3=2·8+3=19
y₅=2y₃+3=2·9+3=21
y₆=2y₄+3=2·19+3=41
y₇=2y₅+3=2·21+3=45
y₈=2y₆+3=2·41+3=85
y₉=2y₇+3=2·45+3=93
А
sin (2x)=0
2x=пи*к
х=пи*к/2
Б
cos(x)cos(2x)-sin(x)sin(2x)=0
cos(x)cos(2x)=sin(x)sin(2x)
существуют формулы
cosAcosB=1/2(cos(A-B)+cos(A+B))
по ней
cos(x)cos(2x)=1/2(cos(x-2x)+COS(X+2X)
cos(x)cos(2x)=1/2(COS(-X)+COS(3X))
cos(x)cos(2x)=1/2(COS(X)+COS(3X)) минус в косинусе исчезает
далее по формуле
sinAsinB=1/2(cos(A-B)-cos(A+B)
по ней
sin(x)sin(2x)=1/2(cos(x)-cos(3x))
получаем
1/2(COS(X)+COS(3X))=1/2(cos(x)-cos(3x)) делим на 1/2
(COS(X)+COS(3X)=(cos(x)-cos(3x))
теперь по формулам сумма и разность косинусов
2cos(2x)cos(x)=-2sin(2x)sin(-x) и выносим минус
2cos(2x)cos(x)=2sin(2x)sin(x) делим на 2
cos(2x)cos(x)=sin(2x)sin(x)
cos(2x)cos(x)-sin(2x)sin(x)=0
cos(2x)cos(x)-2sin(x)cos(x)sin(x) раскрыли синус по формуле двойного угла и вынесем общий косинус
cos(x)(cos(2x)-2sin(x)sin(x))=0
cos(x)=0
х=пи/2 +пи*к
И
cos(2x)-2sin(x)sin(x)=0 раскроем косинус по формуле двойного угла
(1-2sin^2(x))-2sin^2(x)=0
1-4sin^2(x)=0
-4sin^2(x)=-1
sin^2(x)=1/4
sin(x)=1/2 И sin(x)=-1/2
x=пи/6+2пи*к
х=5пи/6+2пи*к
х=7пи/6+2пи*к
х=11пи/6+2пи*к
x=пи/6+2пи*к
х=5пи/6+2пи*к
х=7пи/6+2пи*к
х=11пи/6+2пи*к
х=пи/2 +пи*к