Вероятность выбросить комбинацию {5; 6} складывается из двух возможностей:
- на первом кубике выпало 5, а на втором выпало 6;
- на первом кубике выпало 6, а на втором выпало 5.
Вероятность выпадения каждого числа равна в отдельности:
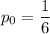
Тогда, вероятность выбросить комбинацию {5; 6} при броске двух кубиков складывается из двух несовместных событий (перечислены выше), каждое из которых представляет собой комбинацию независимых событий (выпадение первого и второго кубика):
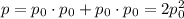

Соответственно, вероятность не выбросить эту комбинацию соответствует вероятности противоположного события:
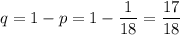
Вероятность не выбросить нужную комбинацию при двух бросках дважды определяется по правилу умножения вероятностей независимых событий:
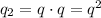
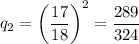
Эта вероятность соответствует ситуации, когда гости не получат комплимент. Значит, противоположное событие - гости получат комплимент, оно произойдет с вероятностью:

ответ: 0.11
найдём производную функции f(x)=2x³ -3x² -1
f'(x)=6x² - 6x
6x² - 6x= 0
6x(x -1) = 0
1) 6x = 0
x₁ = 0
2) x -1=0
x₂ = 1
график функции f'(x)=6x² - 6x представляет собой квадратную параболу веточками ввех, следовательно,
при х∈(-∞; 0] f'(x)> 0 ⇒ f(x) возрастает
при х∈[0; 1] f'(x)< 0 ⇒ f(x) убывает
при х∈[1; +∞) f'(x)> 0 ⇒ f(x) возрастает
в точке х = 0 локальный максимум y mах = -1
в точке х =1 локальный минимум y min = 2 -3 -1 = -2
Забрали-10 шт.
Положили- 14шт
Стало-85
1) x-10+14=85
x-(10+14)=85
x-24=85
x=85-24
x=61
61-10+14=85
ответ: было первоначально 61 гриб.