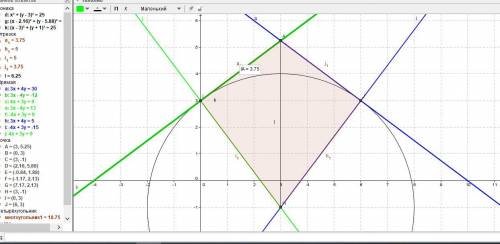
Даны прямые 3х +4y — 30 = 0, 3х – 4y +12 = 0 и окружность радиуса R = 5.
Находим точку пересечения прямых как вершину заданного четырёхугольника.
3х +4y — 30 = 0,
3х – 4y +12 = 0, сложим уравнения.
6х — 18 = 0, х = 18/6 = 3. у = (3х + 12\4 = (3*3 + 12)/4 = 21/4 = 5,25.
Точка А(3; (21/4)).
Находим угол φ между двумя прямыми, заданными общими уравнениями A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0, который вычисляется по формуле:
cos φ = (A1A2 + B1B2)/(√(A1² + B1²)*√(A2² + B2²)).
По формуле находим:
cos φ = (3*3 + 4*(-4)/(√(3² + 4²)*√(3² + (-4)²) = -7/25.
cos φ = -7/25 = -0,28.
φ = arccos(-0,28) = 1,85459 радиан или 106,2602 градуса.
Отрезок, соединяющий вершину А и центр окружности как биссектриса делит этот угол пополам.
Найдём его тангенс.
tg(φ/2) = √((1 - cos φ)/(1 + φ)) = √((1 - (-7/25))/(1 + (-7/25)) = √(32/18) = 4/3.
Теперь можно найти сторону "а" четырёхугольника.
а = R/tg(φ/2) = 5/(4/3) = 15/4 = 3,75.
Площадь четырёхугольника равна площади двух равных прямоугольных треугольников.
S = 2*((1/2)*5*(15/4)) = 75/4 = 18,75 кв.ед.
Пошаговое объяснение:
Гриша встал в 7 часов
Миша а на 13 мин. его раньше , значит Миша встав в :
7 часов - 13 мин.,
помним , что 1 час = 60 мин , по-этому 7 часов утра можно записать как : 6 часов + 60 мин, отсюда Миша встал в :
6 часов + 60 мин - 13 мин = 6 часов 47 мин.
Леша встал на 4 мин.позже чем Миша , значит :
6 час. 47 мин + 4 мин = 6 час +( 47 мин+4 мин= 6 час 51 мин - время , когда встал Леша
Паша встал на 10 мин позже , чем Леша ,значит :
6 час 51 мин + 10 мин = 6 час ( 60+1) мин = 7 час 1 мин - время когда встал Паша
Отсюда очередь будет такой :
1. Миша : 6 час. 47 мин.
2. Леша : 6 час. 51 мин.
3. Гриша : 7 час.
4. Паша : 7 час.1 мин.