Задано координати вершин трикутника ABC: А(11;-5) В(-1;4) С(15;17)
Знайти:
1) рівняння прямої AB у відрізках на осях;
Находим вектор АВ = (-1-11; 4-(-5)) = (-12; 9).
Составляем каноническое уравнение АВ.
АВ: (х - 11)/(-12) = (у + 5)/9. Приводим к общему знаменателю.
9х - 99 = -12у - 60 и получаем уравнение общего вида:
9х + 12у - 39 = 0.
Перенесём свободный член направо и разделим обе части равенства на него.
(9/39)х + (12/39)у = 1.
Здесь (9/39) и (12/39) и есть отрезки, отсекаемые прямой на осях.
2) внутрішній кут A;
Найден вектор АВ = (-12; 9),
модуль равен √((-12)² + 9²) = √(144+81) = √225 = 15.
Находим вектор АС = (15-11; 17-(-5) = (4; 22),
модуль равен √(4² + 22²) = √(16+484) = √500 = 10√5 ≈ 22,36068.
cos A = (-12*4 + 9*22)/(15*10√5) = 150/335,4102 = 0,447214.
A = arccos = 1,107149 радиан или 63,43495 градуса.
3) загальне рівняння висоти CD та її довжину;
Уравнение высоты CD как перпендикуляра к АВ с уравнением 9х + 12у - 39 = 0. имеет в уравнении общего вида коэффициент В и -А.
CD: 12х - 9у + C = 0. Для определения С подставим координаты точка С:
12*15 - 9*17 + C = 0, отсюда С = -180 + 153 = -27.
Уравнение CD: 12х - 9у - 27 = 0.
Длину CD найдём по разности координат точек C и D.
Точку D находим как точку пересечения прямых AB и CD.
АВ: 9х + 12у - 39 = 0|x(9) = 81x + 108y - 351 = 0
CD: 12х - 9у - 27 = 0|x(12) = 144x - 108y - 324 = 0
225x - 675 = 0.
x = 675/225 = 3, y = (27 - 12*3)/9 = -9/9 = -1.
Точка D(3; -1).
Вектор CD = (3-15; -1-17) = (-12; -18).
Длина CD = √((-12)² + (-18)²) = √(144+324) = √468 ≈ 21,6333.
4) рівняння прямої, що проходить через точку B паралельно прямій AC.
У этой прямой направляющий вектор равен вектору АС.
Только подставляем координаты точки В.
BK: (х + 1)/4 = (у - 4)/22. Приводим к общему знаменателю.
22х + 22 = 4у - 16 и получаем уравнение общего вида:
22х - 4у + 38 = 0.
5. M(Z) = 25,6
D(Z)= 112,8
6. а) M(X) = 2,64
б) D(X) = 0,32
Пошаговое объяснение:
5.
1) Для начала надо рассчитать Z и р-вероятность, т.е.:
Z=2X+4Y; р=р(х)*р(у).
1) Z1 = 2*(-5)+4*4 = 6 ; р=0,2*0,4=0,08
Z2 = 2*(-3)+4*4 = 10 ; р=0,1*0,4=0,04
Z3 = 2*1+4*4 = 18 ; р=0,1*0,4=0,04
Z4 = 2*3+4*4 = 22 ; р=0,6*0,4=0,24
Z5 = 2*(-5)+4*6 = 14 ; р=0,2*0,3=0,06
Z6 = 2*(-3)+4*6 = 18 ; р=0,1*0,3=0,03
Z7 = 2*1+4*6 = 26 ; р=0,1*0,3=0,03
Z8 = 2*3+4*6 = 30 ; р=0,6*0,3=0,18
Z9 = 2*(-5)+4*9 = 26 ; р=0,2*0,3=0,06
Z10 = 2*(-3)+4*9 = 30 ; р=0,1*0,3=0,03
Z11 = 2*1+4*9 = 38 ; р=0,1*0,3=0,03
Z12 = 2*3+4*9 = 42 ; р=0,6*0,3=0,18
2) теперь можно найти M(Z) - математическое ожидание (формула на рис. 1), т.е. это сумма всех Z*х
M(Z) = 6*0,08+10*0,04+18*0,04+22*0,24+14*0,06+18*0,03+26*0,03+30*0,18+26*0,06+30*0,03+38*0,03+42*0,18 = 25,6
3) дисперсия D(X) - это сумма всех Z^2*x - M(Z) (рисунок 2)
D(Z) = (6^2*0,08+10^2*0,04+18^2*0,04+22^2*0,24+14^2*0,06+18^2*0,03+26^2*0,03+30^2*0,18+26^2*0,06+30^2*0,03+38^2*0,03+42^2*0,18) - 25,6^2 = 112,8
6.
ПРОД1 = продукция с первого завода
ПРОД2 = продукция со второго завода
P(ПРОД1) = 3/7 = 0,4
P(ПРОД2) = 4/7 = 0,6
A = продукция (изделие) высшего качества
A|ПРОД1 = продукция высшего качества при условии, что продукция с первого завода
P(A|ПРОД1) = 0,85 (85%/100)
A|ПРОД2 = продукция высшего качества при условии, что продукция со второго завода
P(A|ПРОД2) = 0,9 (90%/100)
По формуле полной вероятности
P(A) = P(ПРОД1)*P(A|ПРОД1) + P(ПРОД2)*P(A|ПРОД2) = (0.4)*(0.85) + (0.6)*(0.9) = 0.34 + 0.54 = 0.88
Случайная величина X - число продукций высшего качества из 3 продукций. Данная случайная величина может принимать следующие значения: 0, 1, 2 и 3.
Событие {X=n} означает, что n продукций высшего качества и (3-n) продукций не высшего качества.
Случайная величина X имеет распределение Бернулли (рисунок 3) р - вероятность успеха
q - вероятность неудачи (не появления события)
n - количество появлений события
p = P(A) = 0.88
q = 1 - p = 1 - 0.88 = 0.12
Математическое ожидание
M(X) = np = 3*(0.88) = 2,64
Дисперсия
D(X) = npq = 3*(0.88)*(0.12) = 0,32
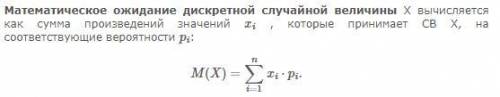

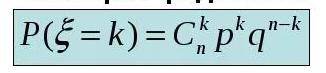
1) А = Б+В-10
2) Б = А+В-14
Сложили эти уравнения и получили 3)
3) А+Б = А+Б + 2*В - 24 сократили (А+Б) и
4) 2*В = 24 и
В= 24:2 = 12 - на третьей полке - ОТВЕТ.