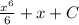
Пошаговое объяснение:
ну согласно свойствам интегралов, коих множество и изучить их надо, чтобы понимать и легко решать, данный интеграл можно представить следующим образом:

это уже сумма двух табличных интегралов.
Заглядываем в таблицу интегралов, которую Вы должны выучить наизусть как таблицу умножения и уже должна быть выучена наизусть таблица производных.
Это опять же, если Вы хотите легко и хорошо решать такие примеры.
В таблице находим похожий интеграл:
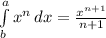
подставляем наши значения по аналогии в данный табличный пример и получаем:
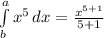
и со вторым выражением также:
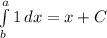
Вот и решили, осталось записать всё в одну строчку:
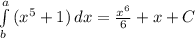
Доказательство.
Пусть α и β — данные плоскости, a1 и a2 — пересекающиеся прямые в плоскости α , а b1 и b2 — соответственно параллельные им прямые в плоскости β .
Допустим, что плоскости α и β не параллельны, то есть, они пересекаются по некоторой прямой c .
Прямая a1 параллельна прямой b1 , значит, она параллельна и самой плоскости β .
Прямая a2 параллельна прямой b2 , значит, она параллельна и самой плоскости β (признак параллельности прямой и плоскости).
Прямая c принадлежит плоскости α , значит, хотя бы одна из прямых — a1 или a2 — пересекает прямую c , то есть имеет с ней общую точку. Но прямая c также принадлежит и плоскости β , значит, пересекая прямую c , прямая a1 или a2 пересекает плоскость β , чего быть не может, так как прямые a1 и a2 параллельны плоскости β .
Из этого следует, что плоскости α и β не пересекаются, то есть, они параллельны.
Свойства параллельных плоскостей
Теорема 1. Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.
Это ответ 2 млн+300 тыс+9 тыс +1