x € [-4; 1] U [2; +oo)
Пошаговое объяснение:
Метод треугольника рулит!
|A| = 6*1*2 + 3*0*4 + 2x(x+2)(x-1) - 4*1(x-1) - 6*0(x+2) - 3*2*2x ≥ 0
Вычисляем:
12 + 0 + 2x^3 + 4x^2 - 2x^2 - 4x - 4x + 4 - 0 - 12x ≥ 0
Приводим подобные:
2x^3 + 2x^2 - 20x + 16 ≥ 0
Делим всё на 2:
x^3 + x^2 - 10x + 8 ≥ 0
Раскладываем на множители:
x^3 - x^2 + 2x^2 - 2x - 8x + 8 ≥ 0
Выделяем первую скобку:
x^2*(x-1) + 4x(x-1) - 16(x-1) ≥ 0
(x-1)(x^2 + 2x - 8) ≥ 0
Раскладываем окончательно:
(x-1)(x-2)(x+4) ≥ 0
По методу интервалов
x € [-4; 1] U [2; +oo)
5х + 13у - 29 = 0
Пошаговое объяснение:
2x + 3y - 8 = 0 и x - 4y +5 = 0
2х + 3у - 8 = х - 4у + 5
2х - х + 3у + 4у = 5 + 8
х + 7у = 13
система уравнения:
х = 13 - 7у
x - 4y +5 = 0
х = 13 - 7у
13 - 7у - 4у + 5 = 0
х = 13 - 7у
-11у = -18
у = 18/11
х = 13 - 7 * (18/11) = 17/11
Значит, точка пересечения двух прямых М2 (х₂;у₂) имеет координаты (17/11; 18/11)
Точка М1 (х₁;у₁) = (-2; 3)
Уравнение прямой, проходящей через эти точки имеет такой вид:
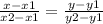
или
(х-х₁)(у₂-у₁)=(у-у₁)(х₂-х₁)
(х - (-2))(18/11 - 3) = (у - 3)(17/11 - (-2))
(х+2)*(-15/11) = (у-3)*(39/11)
-15х/11 - 30/11 = 39у/11 - 117/11
-15х/11 - 39у/11 - 30/11 + 117/11 = 0 (умножить на 11, чтобы избавиться от дробей)
-15х - 39у + 87 = 0 (разделить на -3)
5х + 13у - 29 = 0