радиус окружности, вписанной в трапецию, равен половине высоты этой трапеции. (диаметр окружности d равен высоте трапеции)
Если в трапецию вписана окружность, значит сумма противоположных сторон этой трапеции равна.
То есть ВС+AD=AB+CD
1+6=AB+4 ⇒ AB=3
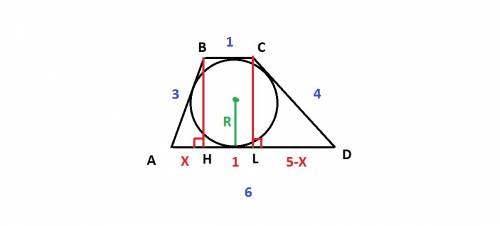
проведем две высоты: ВН и CL
BCLH - прямоугольник, значит BC=HL=1
Если AD=6, то AH+LD=AD-HL=6-1=5
Пусть AH=x , тогда LD=5-x
ВН = CL=h -высоты
Рассмотрим ΔABH и ΔCDL - они прямоугольные, значит для них действует теорема Пифагора
BH²=AB²-AH²
h²=3²-x²
CL²=CD²-LD²
h²=4²-(5-x)²
составляем систему:
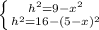
левые части равны, значит приравниваем правые:
9-х²=16-(5-x)²
9-х²=16-25+10х-х²
10х=18
х=1,8
h²=9-x²=9-1.8²=5.76
h=√5.76=2.4
d=h=2.4
C=2πR=πd=2.4π≈2.4*3.14=7.536
ОТВЕТ: 2,4π см или ≈7.536 см
Пошаговое объяснение:
во всех случаях пользуемся формулой
f(x₀+ Δx) ≈ f(x₀) + f'(x₀)*Δx
теперь надо просто найти "хорошие" х₀ и Δх
в первом случае
х₀ = 45°; Δх = 1° = π/180
вот теперь вычисляем
sin 46° = sin (45° + 1°).
f'(x) = (sin x)' = cos x
sin 46° ≈ sin 45° + cos(45°) * π/180 = 1/√2 + (1/√2) * π/180 =
= (1 + π/180) / √2 ≈ (1 + 3.14/180) / 1.41 ≈ 0.7216 ≈ 0.72
во втором случае х₀ = 216; Δх = 71
f'(∛x) = 1/ 3*∛x²
f(∛216) = 6
f'(∛216) = 1/3*∛216²
дальше по формуле вычисляем
в третьем случае х₀ = 0,5; Δх = 0,01
f'(arccos x) = -1 /√(1-x²)
ну и дальше по формуле
9x+x+2x-10 = 10х+2х-10 = 12х-10 = 12*20-10 = 240-10 = 230