Для того чтобы высчитать площадь фигуры неразрывной функции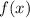 
на некотором промежутке, следует воспользоваться формулой Ньютона — Лейбница:
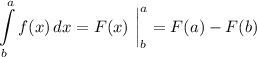
Здесь 
и 
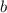— границы фигуры на оси абсцисс, 
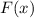— первообразная для функции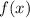
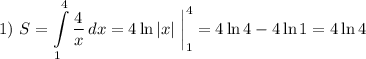квадратных единиц.
2) Здесь имеем площадь фигуры, ограниченной двумя функциям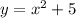и: 
и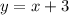 
.
Чтобы найти данную площадь, нужно найти разность площадей каждой функции.
Очевидно, что площадь фигуры, образованной функцией 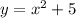на отрезке ![[-2; \ 1]](/tpl/images/1068/9083/4704b.png)
больше, чем площадь фигуры, образованной функцией 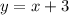на том же отрезке, поэтому
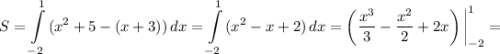
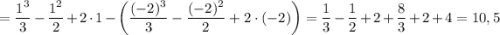квадратных единиц.
11,5-9,2=2,3 2,3/9,2=0,25=25%
цена товара не может понизиться с 44руб до 374 руб.Что-то не так, исправьте второе задание,потом уж решим.
Тогда будем считать, что цена товара с 44 руб. упала до 37,4 руб., отсюда решение второй задачи: 44/37,4=1,17=17%
Третья задача решается по смыслу второй: если цена товара упала на 17%, следовательно прежняя цена была выше на 17% по сравнению с настоящей
Ксюша, посмотри, может такое условие :Цена товара понизилась с 374 руб до 44 руб.? С таким условием решение будет совершенно друим, таким вот :
374руб-100%, 44руб-x% тогда x=44*374^100=12% 100%-12%=88% на 88% снизилась цена товара и , соответственно прежняя стоимость была больше по сравнению с настоящей на 88%.
