Дано уравнение √(2x+4) = 1 - 2x.
ОДЗ: 2x + 4 ≥ 0, х ≥ -2,
1 - 2x ≥ 0, х ≤ 1/2.
Вывод: обе части его - положительны.
Левая часть - возрастающая функция, правая - убывающая.
Значит, есть одна точка пересечения, в которой справедливо равенство (если оно существует).
Возведём его в квадрат: 2x + 4 = 1 - 4x + 4x².
4x² - 6x - 3 = 0. Д = 36 + 4*4*3 = 84. √84 = 2√21.
х1 = (6 + 2√21)/8 = (3 + √21)/4 ≈ 1,89564. По ОДЗ не принимаем.
х2 = (6 - 2√21)/8 = (3 - √21)/4 ≈ -0,39564.
ответ: корень один и равен х = (3 - √21)/4 ≈ -0,39564.
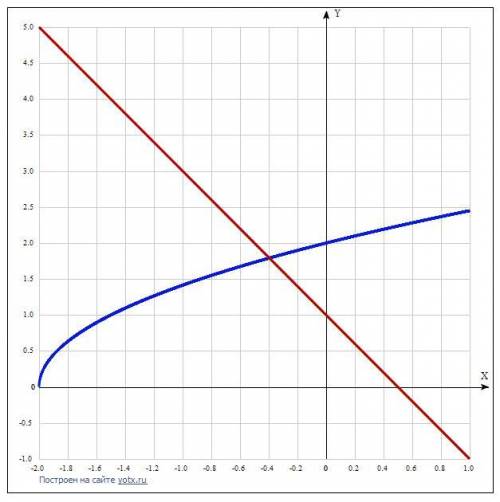
ответ можно подтвердить графически: ведь корень - это точка пересечения двух графиков у = √(2x+4) и у = 1 - 2x.
НОК (5;15) = 15
ЧАСТНЫЙ СЛУЧАЙ!
Т.к 15 делится нацело на 5, наименьшее общее кратное этих чисел равно этому числу: 15 .
НОК (6, 10) = 30
1) Разложим на простые множители 6 = 2 • 3
2) Разложим на простые множители 10 = 2 • 5
3) Выберем в разложении меньшего числа (6) множители, которые не вошли в разложение: 3
4) Добавим эти множители в разложение большего числа 2 , 5 , 3
5) Полученное произведение запишем в ответ. НОК (6, 10) = 2 • 5 • 3 = 30
НОК (12, 20) = 60
1) Разложим на простые множители 12 = 2 • 2 • 3
2) Разложим на простые множители 20 = 2 • 2 • 5
3) Выберем в разложении меньшего числа (12) множители, которые не вошли в разложение : 3
4) Добавим эти множители в разложение большего числа 2 , 2 , 5 , 3
5) Полученное произведение запишем в ответ
НОК (12, 20) = 2 • 2 • 5 • 3 = 60
t - ?
Выражение: 2,4 : (13,2 - 9,6) = 2/3
1) 13,2 - 9,6 = 3,6 (км/ч) - скорость сближения при движении вдогонку;
2) 2,4 : 3,6 = 24/36 = 2/3 (ч) - через 2/3 ч второй лыжник догонит первого.
2/3 ч = (60 : 3 * 2) мин = 40 мин
Вiдповiдь: через 40 хв другий лижник наздожене першого.