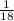= 0,0[5] - не конечная десятичная дробь.
= 
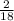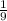= 0,[1] - не конечная десятичная дробь.
= 
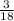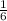= 0,1[6] - не конечная десятичная дробь.
= 
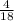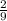= 0,[2] - не конечная десятичная дробь.
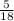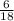= 0,2[7] - не конечная десятичная дробь.
= 
= 0,[3] - не конечная десятичная дробь.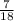
= 0,3[8] - не конечная десятичная дробь.
= 
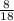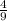= 0,[4] - не конечная десятичная дробь.
= 
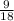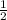= 0,5 - конечная десятичная дробь - 1-ая дробь.
= 
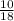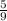= 0,[5] - не конечная десятичная дробь.
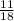= 0,6[1] - не конечная десятичная дробь.
= 
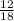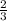= 0,[6] - не конечная десятичная дробь.
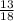= 0,7[2] - не конечная десятичная дробь.
= 
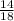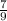= 0,[7] - не конечная десятичная дробь.
= 
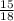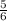= 0,8[3] - не конечная десятичная дробь.
= 
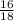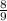= 0,[8] - не конечная десятичная дробь.
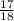= 0,9[4] - не конечная десятичная дробь.
= 
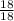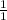= 1 - конечная десятичная дробь - 2-ая дробь. 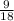= = 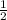0,5 - конечная десятичная дробь - 1-ая дробь. 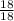= = 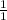1 - конечная десятичная дробь - 2-ая дробь.
4x+5y+4=0 y=(-4x-4)/5 y=-4x/5-4/5
а) 5x-2=-4x/5-4/5
5x+4x/5=-4/5+2
29x/5=6/5
x=6/29 y=5*(6/29)-2=30/29-58/29=-28/29
Точка пересечения прямых (6,29;-28.29)
б) угол между прямыми можно найти по формуле
tgφ=(k₂-k₁)/(1+k₁k₂)
где k₁ и k₂ угловые коэффициенты, в наших уравнения они равны
k₁=5; k₂=-4/5
Проверим будут ли прямые перпендикулярны (условие перпендикулярности прямых 1+k₁k₂=0):
1+5*(-4/5)=1-4=-3≠0 - значит прямые не перпендикулярны
Подставляем значения коэффициентов в формулу нахождения угла:
tgφ=(-4/5-5)/-3=29/15
φ=arctg(29/15) ≈ 1,0934 рад ≈ 63°