Площадь квадрата равна S = a2, значит а = √S. Найдем сначала сторону квадрата, а затем периметр, равный стороне, умноженной на 4.
а) а = √144 = 12 (см).
P = 12 * 4 = 48 (см).
б) а = √64 = 8 (дм).
P = 8 * 4 = 32 (дм).
в) а = √576 = 24 (м).
P = 24 * 4 = 96 (м).
г) Воспользуемся соотношением мер площади 1 ар = 100 м2, 121 ар = 12100 м2.
а = √12100 = 110 (м).
P = 110 * 4 = 440 (м).
д) Аналогично переведем в м2: 1 га = 10 000 м2, 169 га = 1 690 000 м2.
а = √1690000 = 1300 м = 1 км 300м.
P = 1300 * 4 = 5 200 м = 5 км 200 м.
Пошаговое объяснение:
Я отличник
ответ: 350 литров. 375 литров.
Пошаговое объяснение:
Дано. В двух бочках 725 л бензина.
Когда из первой бочки взяли 1/3,
а из второй бочки 2/7 бензина,
то в обеих бочках бензина стало поровну.
Сколько литров бензина было в каждой бочке первоначально?
Решение.
Пусть в 1 бочке было х литров. Когда взяли 1/3 там осталось х- 1/3х=2/3х литров.
Пусть во второй бочке было у литров. Из нее взяли 2/7у литров и осталось у-2/7у=5/7у литров.
Составим систему:
х+у=725;
2/3х = 5/7у;
14х=15у;
х=725-у;
14(725-у)=15у;
10 150-14у=15у;
29у = 10 150;
у=350 литров было во 2 бочке.
х=725 - 350 = 375 литров было в 1 бочке.
Это будет след заданной плоскости, параллельной оси ОУ.
Тангенс угла наклона к оси ОХ равен (3-(-1))/(-3-2) = -4/5.
Находим отрезки на осях координат, отсекаемые искомой плоскостью.
Возьмём точку В1 на прямой А1В1. Она пересекает ОХ на расстоянии 3/(-4/5) = -15/4 = -3,75 от проекции точки В1 на ось ОХ.
-3-(-3,75) =0,75 = 3/4.
На оси OZ точка пересечения равна 0-(0,75*(-4/5) = 0,6 = 3/5.
Если плоскость пересекает оси OX, OY и OZ в точках с координатами (a, 0, 0), (0, b, 0) и (0, 0, с), то она может быть найдена, используя формулу уравнения плоскости в отрезках
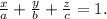
Ось ОУ не пересекается, то есть b=0 и это слагаемое отсутствует.Подставим значения отрезков в уравнение:
После преобразования получим уравнение плоскости: