
Первый трактор в день вспахивает 15 гектаров
Пошаговое объяснение:
Пусть первый трактор вспахивает за 1 рабочий день Х га (Х>0). Тогда, по условию, второй трактор вспахивает за 1 рабочий день (Х - 2,5) га.
Первый трактор вспахивает поле размером 150 га за 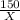 дней, а второй трактор вспахивает за
дней, а второй трактор вспахивает за 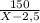 дней.
дней.
На поле размером 150 га первому трактору требуется на два рабочих дня меньше, чем второму, отсюда получаем следующее уравнение:
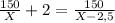
150·(X-2,5)+2·X·(X-2,5)=150·X
150·X-375+2·X²-5·X=150·X
2·X²-5·X-375=0
D=(-5)²-4·2·(-375)=25+3000=3025=55²
X₁=(5-55)/(2·2)= -50/4= -12,5<0 не подходит;
X₂=(5+55)/(2·2)= 60/4 = 15
Первый трактор в день вспахивает 15 гектаров.
ответ: х принадлежит промежутку(7; 7+^3√11), 7 –не входит в промежуток так как неравенство .строгое
Пошаговое объяснение:
До решения заданного неравенства решим уравнение вида
(x-7)^2 = корень из 11*(x-7)
Чтобы избавиться от квадратного корня возведем обе части уравнения в квадрат:
(х-7)^4=11(х-7),
х-7≥ 0, х≥ 7.
Переносим обе части уравнения в одну сторону :
(х-7)^4-11(х-7)=0
(х-7)((х-7)^3-11)=0
Составляем совокупность уравнений:
Х-7=0 или (х-7)^3-11=0
Х=7 или х=7+^3√11
Точки разделяют луч [7;+ ∞) на двапромежутка:
(7; 7+^3√11) и (7+^3√11; +∞), 2,2<^3√11<2,3
На первом промежутке (7; 7+^3√11) исходное неравенство верно, на втором (7+^3√11; +∞) – неверно