Площадь 1-ой фигуры 16см2
Площадь 2-ой фигуры 16см2.
Пошаговое объяснение:
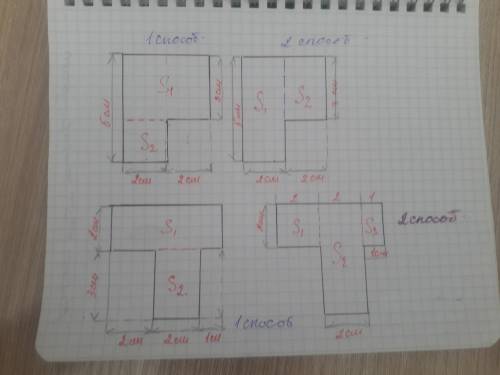
1. Фигура.
:
1 фигуру делим на 1 квадрат со сторонами а = 2см и второй прямоугольник со сторонами а= 3см и b= 4 см.
Теперь находим площади отдельно для каждой фигуры и складываем.
S□= a×4
S= a×b
a1 = 2см
S1= ?
S1= 2см×2см= 4 см2
а2 = 3см
b2 = 4см
S2 =?
S2= 3см × 4см=12 см2
Sобщ= S1+ S2
Sобщ=4+12= 16 см2
.
Эту же 1-ую фигуру делим на 2 прямоугольника со сторонами а1= 5см, b1 = 2см и второй со сторонами а2= 3см, b2 = 2см. Теперь находим площадь фигур по формуле :
S= a×b
a1= 5см
b1= 2см
S1= ?
S1 = 5×2=10 см2
a2= 3см
b2=2см
S2= ?
S2= 3×2= 6 см2
Sобщ= S1+ S2
Sобщ= 10+6= 16 см
2 . Фигура.
.
Находим площадь аналогично нахождению площади первой фигуры .
2см+2см+1см=5см - длина 1 -ой фигуры.
а1 = 5см
b1 = 2 см
S1=?
S1= 5×2= 10см2
а2= 3см
b2= 2см
S2=?
S2= 3×2=6см2
Sобщ= S1+S2
Sобщ= 10+6=16см 2
:
Делим на 3 фигуры : 1 квадрат и 2 прямоугольника и находят площадь аналогично площади предыдущих фигур.
Рисунки прилагаются.
Из исходного равенства видно, что p>q, в противном случае равенство не выполнялось бы. Предположим, что p=q+k, где k - натуральное. Тогда 2q+k=(q+k-q)^3, отсюда 2q+k=k^3 или 2q=k^3-k=k(k^2-1). Тогда q=k(k^2-1)/2. Отсюда сразу видно, что q будет простым только при k=2, поскольку при k=1 получаем 0, а при k>2 будем получать составные числа, а по условию q простое. Итак, при k=2, q=2*(2^2-1)/2=3. Тогда p=q+k=3+2=5. Это единственное решение удовлетворяющее данному равенству.
ответ: p=5, q=3.
Дано: x² - 8*x +y² - 6*y = 0
Найти:
Уравнение окружности: (x+a)² + (y+b)² = R²
S = ?
C = ?
Пошаговое объяснение:
Преобразуем исходное уравнение до квадрата суммы.
1)(x² - 2*4*x +4²) - 16 + (y² - 2*3*y + 3²) - 9 - прибавили и отняли то же самое.
2) (x - 4)² + (y - 3)² = 16+9 = 25 = 5² = R²
Площадь круга по формуле:
S = π*R² = 25*π (ед.²) - площадь - ответ
Длина окружности по формуле:
C = 2*π*R = 10*π (ед.) - длина окружности - ответ.