1) Если параболы имеет вершину в начале координат, то каноническое уравнение параболы имеет вид у² = 2рх.
А уравнение директрисы х + (р/2) = 0.
По заданию уравнение директрисы x+3=0 или х + (6/2) = 0.
Значит, параметр р = 6.
Уравнение параболы у² = 2*6х или у² = 12х.
2) Каноническое уравнение гиперболы имеет вид (x²/a²) - (y²/b²) = 1.
Но у неё действительная ось на оси Ох.+
Для гиперболы с действительной осью на оси Оу уравнение имеет вид -(x²/a²) + (y²/b²) = 1.
По заданию b = 4√5/2 = 2√5.
е = с/b.
Тогда c = e*b=(√5/2)*2√5 = 5.
a² = c² - b² = 25 - 20 = 5.
Уравнение гиперболы -(x²/(√5)²) + (y²/(2√5)²) = 1.
3) а = 10/2 = 5.
с = е*а = 0,6*5 = 3.
b² = a² - c² = 25 -9 = 16 = 4².
Уравнение эллипса (x²/5²) + (y²/4²) = 1.
См. Пошаговое объяснение
Пошаговое объяснение:
Предварительное замечание. Допустим, и у меня, и у тебя по 100 рублей. Если я тебе дам 10 рублей, то у тебя будет на 10 · 2 = 20 рублей больше, чем у меня, так как 110 - 90 = 20. А две эти задачи - обратные той, которую я привёл. В них вопрос ставится так: если у нас с тобой денег было поровну, а я тебе сколько-то дал, после чего у тебя стало на 20 руб. больше, чем у меня, то сколько же я тебе дал? Решение: 20 : 2 = 10 руб. В конце каждой задачи, для проверки, приводится пример расчета, который записывать не надо, а только убедиться в том, что ошибки в расчетах нет.
Задача 1.
(5 3/5 + 1 1/5) : 2 = 6 4/5 : 2 = 3 2/5
ответ: надо перелить 3 2/5 л меда.
Проверим полученный ответ на конкретном примере.
Допустим, в первой бочке 15 3/5 л во второй бочке 10 л.
Из первой бочки переливаем во вторую бочку 3 2/5 л меда.
15 3/5 - 3 2/5 = 12 1/5 - стало в первой бочке
10 + 3 2/5 = 13 2/5 - стало во второй бочке
В первой бочке стало меньше, чем во второй, на:
13 2/5 - 12 1/5 = 1 1/5 л - что соответствует условию задачи.
Задача 2.
(8 1/4 - 5 3/5) : 2 = ((7-5) + (5/4 - 3/5)) : 2 = (2 13/20) : 2 = 1 13/40
ответ: надо перелить 1 13/40 л меда.
Проверим полученный ответ
Допустим, в первой бочке было 15 3/5 л, а во второй 10 л. Из второй бочки переливаем в первую бочку 1 13/40 л меда, получаем:
10 - 1 13/40 = (9-1) + (40/40 - 13/40) = 8 27/40 - стало во второй бочке
15 3/5 + 1 13/40 = (15+1) + (3/5 + 13/40) = 16 37/40 - стало в первой бочке
16 37/40 - 8 27/40 = 8 10/40 = 8 1/4 л - что соответствует условию задачи.
Если имеется в виду объём шара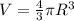 , то
, то
ответ: радиус шара равен 1.