Для того, чтобы представить в виде многочлена выражение (5 + 2y)(y^2 + 2y - 3) мы прежде всего выполним умножения многочлена на многочлен.
Итак, выполняем умножения и получаем выражение равносильное заданному:
(5 - 2y)(y^2 + 2y - 3) = 5 * y^2 + 5 * 2y - 5 * 3 - 2y * y^2 - 2y * 2y + 2y * 3 = 5y^2 + 10y - 15 - 2y^3 - 4y^2 + 6y.
Нам теперь нужно выполнить группировку и приведение подобных слагаемых в полученном выражении:
5y^2 + 10y - 15 - 2y^3 - 4y^2 + 6y = -2y^3 + 5y^2 - 4y^2 + 10y + 6y - 15 = 3y^2 - 4y^2 + 16y -15.
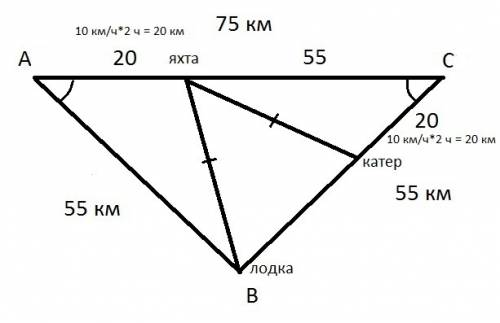
Имеем равнобедренный треугольник, углы в основании которого А и С равны, стороны по 55 км и основание 75 км.
После посадки на мель, маршруты к яхте и пройденные пути, образовали два равных треугольника, по признаку: если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны (смотри схему). Пути катера и лодки равны, скорости равны – 20 км/час. Значит, к яхте, они прибудут одновременно, если лодка вышла одновременно со сменой курса катером. (В условии об этом не сказано.)