Пошаговое объяснение:
1) Берешь любые числа, которые подходят, чтобы при х-y = 8
это может быть, как я взяла х = 10, y = 2, может x = 9, тогда y = 1
и доп уравнение было бы x+y= 10
2) Оба уравнения должны быть одинаковыми, тогда и решение у них будет любое
потому что , если сократить 2х-2y = 16
2(x-y) = 16
x-y = 8, как и в условии
т.е ещё варианты: 3x-3y=24, 4x-4y=32 и т.д.
3) система не имеет решений тогда, когда два одинаковых уравнения равны разным числам
т.е. x-y = можно написать любое понравившееся число
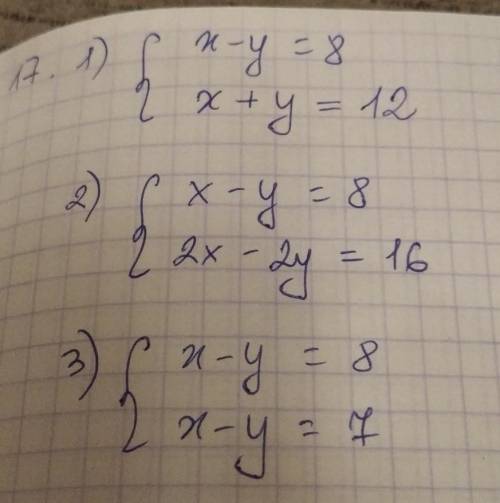
9 одноклассников у Кати.
Пошаговое объяснение:
Решать можно по разному.
Первый вариант решения
Первый алгебраический, уравнением:
Пусть,
х - искомое число одноклассников Кати.
Заметим, что Катя в это число не входит, т.е
всего детей в классе (х+1) человек.
а - количество конфет у Артема после 1-ой раздачи.
Тогда у самой Кати после 1-ой раздачи:
а + 10 конфет
После Катя дала каждому (включая Артема) по 1 конфете. Т.е. раздала во второй раз Катя
х конфет
И у Артема и остальных окончательно оказалось
а + 1 конфет
Нам известно, что у самой Кати от (а + 10) конфет осталось, сколько у всех, (а + 1). А значит,
(а + 10) - х = (а + 1)
сокращаем а:
10 - х = 1
х = 9
ответ: 9 одноклассников у Кати.
Альтернативное решение
По условию задачи ясно, что совершенно неважно, сколько конфет вначале у Артема. Для удобства представим, что Катя жадина, и у Артема 0 конфет вначале. А у Кати на 10 больше. Значит, Катя имеет
0 + 10 = 10 конфет.
Которые по одной и раздает всем, включая саму себя.
А значит - всего ребят 10, включая жадную Катю. А одноклассников Кати
10 - 1 = 9 человек.
д) -2 5/14 + 3 4/21 = 3_8/42 - 2_15/42 = 2_50/42 - 2_15/42 = 35/42 = 5/6
е)- 5 13/15 - 11.18 = - (5_13/15+11_18/100)= -(5_130/150 + 11_27/150)= - 16_157/150 = -17_7/150