(0;2]U[4;6)
Пошаговое объяснение:
ОДЗ:
{x > 0;
{6–x > 0 ⇒ x < 6
{(x4–12x3+36x2) > 0⇒ (x·(6–x))2 > 0 ⇒ x≠0; x≠6
ОДЗ: х∈(0;6)
при х∈(0;6):
log2(x4–12x3+36x2)=log2x2·(6–x)2=
log2(x·(6–x))2=2log2x·(6–x)=2log2x+2log2(6–x)
Неравенство принимает вид:
(2–log2x)·(log2(6–x)–2) ≥ 0
Применяем обобщенный метод интервалов
log2x=2 или log2(6–x)=2
x=4 или 6–х=4;х=2
При х=1
(2–log21)·(log2(6–1)–2)=2·(log25–log24) > 0
При х=3
(2–log23)·(log2(6–3)–2)=–(2–log23)2 < 0
При х=5
(2–log25)·(log2(6–5)–2)=(log24–log25)·(0–2) > 0
(0)__+__ [2]__–__[4]__+__ (6)
1. Пусть собственная скорость катера х км/ч, а скорость течения у км/ч, то составим и решим систему уравнений:
0,5(х+у)=4,5
х+у=1,5(х-у)
х+у=9
х-5у=0
6у=9, у=1,5
Значит скорость течения 1,5 км/ч
2. Пусть в первый день мастер изготовил х деталей, а ученик - у деталей, то составим и решим систему уравнений:
х+у=100
1,2х+1,1у=116
х=100-у
1,2(100-у)+1,1у=116
120-1,2у+1,1у=116
0,1у=4
у=40, х=60
Значит в первый день мастер изготовил 60 деталей, а ученик - 40 деталей.
3. Пусть карандаш стоит х тенге, тетрадь - у тенге, то
8х+5у=417
2х+у=93
8х+5у=417
-8х-4у=-372
у=45, х=24
Карандаш стоит 24 тенге, а тетрадь 45 тенге
4. Пусть велосипедист должен был ехать со скоростью х км/ч, то
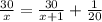
600(x+1)-600x-x^2-x=0
x^2+x-600=0
D=1+2400=2401
x1=(-1+49)/2=24, x2=(-1-49)/2=-25 - не удовлетворяет условию задачи
Значит велосипедист должен был ехать со скоростью 24 км/ч, а ехал со скоростью 25 км/ч
4. Пусть двухместных лодок х штук, а трехместных - у штук. то
х+у=6
2х+3у=14
у=2, х=4
Значит двухместных 4 лодки, а трехместных 2 лодки
Получился прямоугольник с вершинами:
А(1,-3), B(4,0), C(2,2), D(-1,-1) графики в приложении.
Благодарим предка Пифагора и вычисляем стороны прямоугольника.
Длина - а =АВ =√9²+9² = 3√2
Ширина -b =BC = 2*√2
И площадь - S =a*b = 3*√2 * 2*√2 = 6*2 = 12 ед² - ОТВЕТ.