а) 2,2,4
б) нет. Наименьшее из написанных чисел - наименьшее из загаданных чисел; наибольшее - сумма загаданных чисел. Так, среди загаданных чисел есть 1, а сумма всех чисел равна 22. Но сумма всех чисел без единицы 22-1=21 не выписана.
в) Сумма чисел 52. Наименьшее число равно 9. 10, 11 - также загаданные числа (это не может быть суммой 9 и какого-то числа, не меньшего 9).
19 = 10 + 9; 43 = 52 - 9
20 = 11 + 9; 42 = 52 - 10
21 = 10 + 11; 41 = 52 - 11
22 = ? 33 = 52 - 10 - 9
30 = 52 - 22; 32 = 52 - 11 - 9
31 = 52 - 10 - 11
Рассмотрим случаи.
а) Число 22 среди загаданных. Тогда 30=52-22, загаданные числа 9, 10, 11, 22 - их сумма 52, и все "частичные суммы" выписаны.
б) Число 22 не среди загаданных. Тогда 22 - какая-то сумма составленная из чисел 9, 10, 11 (взятыми произвольное (возможно, нулевое) число раз).
9 не может входить в эту сумму (22-9=13 невозможно получить сложением этих чисел).
Аналогично, 10 не входит в эту сумму. Итак, 22 = 11 + 11 и 11 взято как минимум 2 раза.
Уже известные числа: 9, 10, 11, 11 - сумма 41. Оставшееся число равно 52-41=11. Легко проверить, что этот набор чисел также удовлетворяет условию.
ответ.
а) 2,2,4
б) нет
в) {9, 10, 11, 22} или {9, 10, 11, 11, 11}
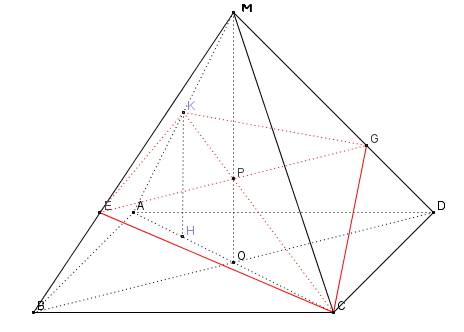
обозначим середину ребра МА точкой K.
О - точка пересечения диагоналей основания, т.е. МО - высота пирамиды;
точка E - середина MB, точка G - середина MD;
P - точка пересечения диагоналей KGCE;
KH - перпендикуляр, опущенный от точки K на прямую AC
MO и CK - медианы треуголника AMC⇒MP/MO=2/3
△MEG∼△MBD⇒EG=2/3BD.
EKGC - четырехугольник, диагонали которого - перпендикулярны: BD⊥MO,BD⊥AC⇒BD⊥(MAC)⇒BD⊥CK.
Так как EG||BD, значит EG⊥CK
CH=3/4AC,KH=1/2MO ( KH - средняя линия треугольника AMC), CK= (CH^2+KH^2) под корнем ( по теореме Пифагора)
( а дальше я не знаю...)
1)Часть единицы или несколько её частей называются обыкновенной или простой дробью. Количество равных частей, на которые делится единица, называется знаменателем, а количество взятых частей – числителем. Дробь записывается в виде:
2)Здесь 3 – числитель, 7 – знаменатель.
Если числитель меньше знаменателя, то дробь меньше 1 и называется правильной дробью. Если числитель равен знаменателю, то дробь равна 1. Если числитель больше знаменателя, то дробь больше 1. В обоих последних случаях дробь называется неправильной. Если числитель делится на знаменатель, то эта дробь равна частному от деления: 63 / 7 = 9. Если деление выполняется с остатком, то эта неправильная дробь может быть представлена смешанным числом:
3)Здесь 9 – неполное частное (целая часть смешанного числа), 2 – остаток (числитель дробной части), 7 – знаменатель.
Часто бывает необходимо решать обратную задачу – обратить смешанное число в дробь. Для этого умножаем целую часть смешанного числа на знаменатель и прибавляем числительдробной части. Это будет числитель обыкновенной дроби, а знаменатель остаётся прежним.
Обратные дроби – это две дроби, произведение которых равно 1. Например, 3 / 7 и 7 / 3 ; 15 / 1 и 1 / 15 и т.д.