а) Обозначим точки пересечения лучей с отрезком BM — буквами P и R (см. рисунок), и пусть O — точка пересечения диагоналей параллелограмма, а N — точка пересечения луча AP и прямой BC.
Точка R делит медиану BM треугольника ABD в отношении 2 :1 считая от B. Следовательно, R лежит на медиане AO этого треугольника, то есть луч AR содержит диагональ AC .
б) Пусть L — точка пересечения AN и BD. Нужно найти площадь четырёхугольника LNCO. Пусть площадь параллелограмма равна S . Площадь треугольника BOC равна Найдём площадь треугольника BNL . Из подобия треугольников BPN и MPA следует, что
откуда
Теперь из подобия треугольников BNL и DAL следует, что их соответствующие высоты относятся как 1:4 , а поэтому высота треугольника BNL, проведённая к BN, составляет высоты параллелограмма, проведённой к стороне BC.
Поэтому
Следовательно, площадь четырёхугольника LNCO равна
Пошаговое объяснение:
Основные правила:
Высоты (в ПТ являющаяся и медианами, и биссектрисами) , проведенные из вершин правильного треугольника, делятся точкой пересечения в соотношении 2:1, считая от вершины треугольника
Радиус окружности, описанный около ПТ в два раза больше радиуса вписанной окружности (вывод из предыдущего правила)
1. По теореме Пифагора найдем высоту треугольника (медиану)
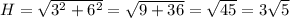 см
см
Также Н = 2k+k = 3k
3k = 3√5
k = √5
Значит:
R = 2*√5 = 2√5 см
r = √5 см
2. R = 2*9 = 18 см
H = 18+9 = 27 см
Есть формула для нахождения стороны ПТ через высоту (следствие из теоремы Пифагора):
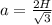
a= 2*27 / √3 = 18√3 cм