Пошаговое объяснение:
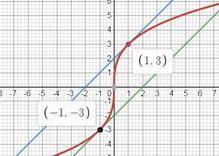
ну, судя по предлагаемым точкам у нас функция
![\displaystyle f(x) = 3 \sqrt [3]{x}](/tpl/images/4257/3722/63eb3.png)
рассмотрим уравнение касательной y = kx +b
здесь к - коэффициент наклона, он же tg угла наклона, он же производная в точке касания
нас интересует угол π/4. tg(π/4) = 1, значит надо найти точку, в которой значение производной будет =1
![\displaystyle f'(x) = \frac{1}{\sqrt[3]{x^2} }](/tpl/images/4257/3722/b2311.png)
![\displaystyle \frac{1}{\sqrt[3]{x^2} } =1 \quad \Rightarrow x_1=1; y_1=3; \quad x_2=-1;y_2= -3](/tpl/images/4257/3722/2aa7d.png)
вот мы получили две точки, в которых касательная будет наклонена к оси ох под углом π/4 M(-1; -3) и N(1; 3)
уравнения касательных
у нас есть уравнение у = кх +b
для нахождения уравнений двух касательных подставим поочередно в это уравнение координаты точек М и N
-3 = -1 + b ⇒ b = -2 ⇒ y₁ = x-2
3 = 1 +b ⇒ b = 2 ⇒ y₂ = x+2