Борын-борын заманда булган икән, ди, бер кеше. Бу кеше нең исеме Нарый булган, ди.
Көннәрдән беркөнне Нарый чыгып киткән, ди, юлга. Бара да бара, ди, бу. Бара торгач барып кергән, ди, бу ялтырап торган боз өстенә. Боз өстенә барып керүе булган, аягы таеп, әйләнеп төшүе булган.
— Боз, син нидән болай көчле?
— Көчле булсам,— ди Боз,— мине Кояш эретә алмас иде, — ди.
— Кояш, син нидән көчле? — ди Нарый.
— Көчле булсам, мине Болыт капламас иде.
— Болыт, син нидән көчле?
— Көчле булсам, мине Яңгыр тишеп чыкмас иде.
— Яңгыр, син нидән көчле?
— Көчле булсам,— ди Яңгыр,— мине Җир сеңдермәс иде.
— Җир, син нидән көчле?
— Көчле булсам, мине Үлән тишеп чыкмас иде.
— Үлән, син нидән көчле?
— Көчле булсам, мине Сыер ашамас иде.
— Сыер, син нидән көчле?
— Көчле булсам, мине Пычак кисмәс иде. Хәзер Пычактан сорый инде Нарый:
— Пычак, син нидән көчле?
— Көчле булсам, мине Ут эретмәс иде.
— Ут, син нидән көчле?
— Көчле булсам, мине Су сүндермәс иде.
— Су, син нидән көчле?
— Көчле булсам, мине кеше җиңмәс иде, ә ул мине җиңә, тегермәннәр әйләндерергә җигә! — ди Су.
Шуннан соң Нарый, кешедән дә көчле нәрсә юк икән дип, үз юлына китә, шуның белән әкият тә бетә.
ДАНО
Y(x) = 16*x² + 32*x
1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная.
Вертикальной асимптоты нет.
2. Пересечение с осью Х. Y=0 при х = - 0,387, - 1,612.
Положительна - X∈(-∞;-1,6)∪(-0,38;+∞),
отрицательна - X∈(-1,612;-0,387).
3. Пересечение с осью У. У(0) = 100.
4. Поведение на бесконечности.limY(-∞) = + ∞ limY(+∞) = +∞
Горизонтальной асимптоты нет.
5. Исследование на чётность.Y(-x) ≠ - Y(x).
Функция общего вида.
6. Производная функции.Y'(x)= 32*x +32 = 32*(x+1).
Корни при Х= - 1.
7. Локальные экстремумы.
Минимум – Ymin(-1)=-6.
8. Интервалы возрастания и убывания.
Возрастает - Х∈[-+;+∞], убывает = Х∈(-∞;-6].
8. Вторая производная - Y"(x) = 32
Точки перегиба нет.
9. Вогнутая – «ложка» во всем интервале определения.
10. График в приложении.
ДАНО
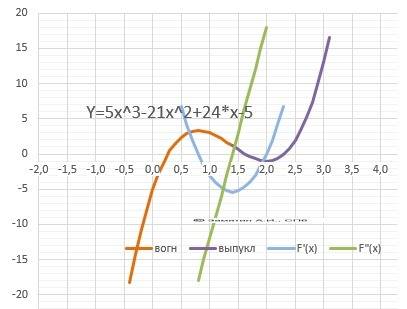
Y(x) = 5x³ - 21*x² + 24*x - 5.
1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная.
Вертикальные асимптоты - нет.
2. Пересечение с осью Х. Y=0 при х = 0,266, 1,63, 2,31.
Положительна - X∈(0,266;1,63)∪(2,31;+∞),
отрицательна - X∈(-∞;0,266)∪(1,633;2,31).
3. Пересечение с осью У. У(0) = -5.
4. Поведение на бесконечности.limY(-∞) = -∞ limY(+∞) = +∞
5. Исследование на чётность.Y(-x) ≠ - Y(x).
Функция ни чётная ни нечётная - общего вида.
6. Производная функции.Y'(x)= 15*x² - 42*х + 24
Корни производной: при Х= 0,8 и 2.
7. Локальные экстремумы.
Максимум Ymax(0,8)= 3,32, минимум – Ymin(2)=-1.
8. Интервалы возрастания и убывания.
Убывает - Х∈[0,8;2], возрастает = Х∈(-∞;0,8]∪[2;+∞).
8. Вторая производная - Y"(x) = 30*x - 42 =0.
Корень производной - точка перегиба Y"(x)= 0,16.
9. Выпуклая “горка» Х∈(+∞;0,16), Вогнутая – «ложка» Х∈(0,16;+∞).
10. График в приложении.
Поясню .
Берём простой лист А4, сворачиваем его в трубку .
Итог - его ширина становится много больше его длинны .
Пусть это новая фигура, но по сути это тот же лист формата А4 ..