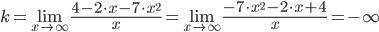Не надо так делать. Фотомас наваливает много воды
Решай тем как я тебе показал в задании.
1. К примеру, есть 5^(x+1)
2. Знаем основное свойство степеней: при умножении двух одинаковых оснований их показатели складываются а основание остается прежним
3. Распишем 5^(x+1) по этому свойству, возьмя за основание 5:
5^x * 5^1, тогда по свойству выходит, что основание равно 5, а степень х +1
Ну и также с 5^(x-2), только вместо 1 в степени будет 5^-2
4. Потом выносишь за скобки 5^x , а в скобках у тебя остаются числа без переменных, делаешь с ними действия и делишь полученное число на то,, которое справа (здесь 122)
Им кстати в конце все равно бы пришлось расписывать степень ;)
Пошаговое объяснение:
1) Область определения функции. Точки разрыва функции.
2) Четность или нечетность функции.
y(-x)=
Функция общего вида
3) Периодичность функции.
4) Точки пересечения кривой с осями координат.
Пересечение с осью 0Y
x=0, y=
Пересечение с осью 0X
y=0
4-2·x-7·x2=0
Нет пересечений.
5) Исследование на экстремум.
y = 4-2*x-7*x^2
1. Находим интервалы возрастания и убывания. Первая производная.
f'(x) = -14·x-2
Находим нули функции. Для этого приравниваем производную к нулю
-14·x-2 = 0
Откуда:
x1 = -1/7
В окрестности точки x = -1/7 производная функции меняет знак с (+) на (-). Следовательно, точка x = -1/7 - точка максимума.
2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.
f''(x) = -14
Находим корни уравнения. Для этого полученную функцию приравняем к нулю.
-14 = 0
Для данного уравнения корней нет.
6) Асимптоты кривой.
y = 4-2·x-7·x2
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты: