Для построения диаграммы Венна для чисел от 10 до 30 по признаку деления на 3 и на 4, в качестве основного множества имеем множество натуральных чисел х, для которых справедливо соотношение: 10 ≤ х ≤ 30. Тогда подмножество А будет состоять из чисел {12; 15; 18; 21; 24; 27; 30}, а подмножество В будет состоять из чисел {12; 16; 20; 24; 28}. Составим подмножество С = А∩В, являющееся пересечением подмножеств А и В, выбрав общие элементы этих подмножеств: С = {12; 24}.
Начертим диаграмму Венна. Для этого нарисуем круг, изображающий подмножество А. Рядом начертим круг, изображающий подмножество В таким образом, чтобы он частично перекрывал первый круг, так как у этих подмножеств есть два общих элемента. Пересечение кругов А и В дают нам подмножество С.
Для построения диаграммы Венна для чисел от 10 до 30 по признаку деления на 3 и на 4, в качестве основного множества имеем множество натуральных чисел х, для которых справедливо соотношение: 10 ≤ х ≤ 30. Тогда подмножество А будет состоять из чисел {12; 15; 18; 21; 24; 27; 30}, а подмножество В будет состоять из чисел {12; 16; 20; 24; 28}. Составим подмножество С = А∩В, являющееся пересечением подмножеств А и В, выбрав общие элементы этих подмножеств: С = {12; 24}.
Начертим диаграмму Венна. Для этого нарисуем круг, изображающий подмножество А. Рядом начертим круг, изображающий подмножество В таким образом, чтобы он частично перекрывал первый круг, так как у этих подмножеств есть два общих элемента. Пересечение кругов А и В дают нам подмножество С.
Пошаговое объяснение:
Экскаватор может выполнить определенную работу за 2 минуты , другой экскаватор может выполнить ту же работу за 4 минуты ,а третий - за 6 минут . За какое время три экскаватора вместе смогут выполнить ту же самую работу?
Примем объём работы за 1, тогда производительность равна:
1/2 работы за минуту - первый экскаватор;
1/4 работы за минуту - второй экскаватор;
1/6 работы за минуту - третий экскаватор.
Совместная производительность экскаваторов равна:
1/2 + 1/4 + 1/6 = 6/12 + 3/12 + 2/12 = 11/12
Найдём время, за которое экскаваторы смогут совместно выполнить ту же самую работу:
1 : 11/12 = 12/11 =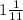 (мин)
(мин)