Решение: Запишем ОДЗ: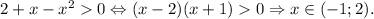 
Переходим к уравнению-следствию: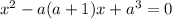 
.
Найдём дискриминант: ![D=[-a(a+1)]^2-4\cdot1\cdot a^3=a^4+2a^3+a^2-4a^3=a^4-2a^3+a^2=a^2(a^2-2a+1)=a^2(a-1)^2=[a(a-1)]^2.](/tpl/images/2005/6762/e07c3.png)
Дискриминант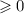 
при любых значениях параметра, а значит квадратное уравнение всегда имеет корень. При 
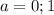дискриминант равен 0 и уравнение имеет единственное решение. Такой вариант нас не устраивает, поэтому будем рассматривать все 
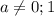. Для них квадратное уравнение имеет два корня:
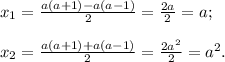
Чтобы исходное уравнение имело два корня необходимо, чтобы оба корня удовлетворяли ОДЗ, т.е.
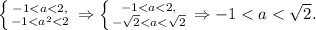
Не забудем исключить 0 и 1 из данного промежутка значений и получим окончательный ответ.
ОТВЕТ: при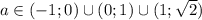 
.
Пошаговое объяснение: Док-во от противного: Пусть дана трапеция АВСД, где АВ-одна из боковых сторон, пусть МК-средняя линия трапеции, является диаметром, М-середина АВ, АМ=МА=х, М-точка касания окружности и боковой стороны, О-центр окружности, тогда ОМ =r. Рассмотрим ΔАОВ, он прямоугольный, т.к. ∠А+∠В=180°(сумма внутр односторон углов при параллельн основаниях, и центр окружностиО-точка пересечения биссектрис углов. ⇒∠ВАО+∠АВО=90° ⇒∠ВОА=90° Т.к. М-точка касания, то ОМ⊥АВ . Из ΔАОВ ⇒ВМ/ОМ == ОМ/АМ , т.е. х/r=r/x ⇒r²=x²⇒ r=x⇒ ΔАОМ прямоуг и равнобедренный ⇒∠МАО=∠МВО=45°⇒∠А=∠В=90°,что невозможно, значит средняя линия не может быть диаметром., чтд
