Пошаговое объяснение:
1)
Для начала вычислим сумму. Для этого приведем дроби к общему знаменателю и сложим
2целых 13/14 + 1целая 20/21 = 2целых 39/42 + 1целая 40/42 = 3целых 79/42 = 4целых 37/42
Теперь нужно найти обратное число. Чтобы найти обратное число, нужно перевести правильную дробь в неправельную
4целыз 37/42 = 205/42
А затем поменять местами числитель и знаменатель 205/42 -> 42/205
40/205 и есть обратное число
2)
8целых 3/4 - 7целых 5/6 = 8целых 9/12 - 7целых 10/12 = 7целых 21/12 - 7целых 10/12 = 11/12
11/12->12/11
12/11=1целая 1/11
3)
1целая 1/15 × 5/16 = 16/15 × 5/16 = 1/3 × 1/1 = 1/3
1/3-> 3/1
3/1 = 3
41472
Пошаговое объяснение:
Пусть d - количество дней, c - количество деталей в день, b - количество заказчиков.
1 условие: "Когда треть продукции одного дня была упакована в ящики, то в каждом ящике оказалось столько деталей, сколько ящиков понадобилось для упаковки, причем число ящиков равно числу дней работы цеха. "
Треть продукции одного дня = c/3.
Число упакованных ящиков = числу деталей в ящике = числу дней работы цеха = d.
Получается, что упаковали d*d=d² деталей. Тогда c/3=d² или c=3d².
2 условие: "После отсылки половины всех деталей заказчикам выяснилось, что куб числа заказчиков был равен числу деталей, высланных каждому из заказчиков."
Половина всех деталей = cd/2
Куб числа заказчиков = b³
Число деталей, высланных каждому (в предположении, что оно одинаковое для каждого заказчика) = cd/2/b=cd/(2b).
Тогда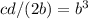 
или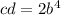 
.
Требуется найти минимальное положительное значение cd.
В выражение 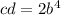вместо c подставим 3d². Тогда:
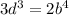
Требуется найти минимальное положительное решение этого уравнения. Заметим, что левая часть делится на 3, а правая на 2. Значит, каждая из частей должна делиться и на 2, и на 3. Тогда d и b можно представить в виде произведения степеней чисел 2 и 3 (другие множители нет смысла рассматривать, так как мы минимизируем ответ).
Пусть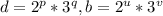 
.
Тогда левая часть равна:
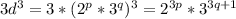
Правая часть равна:
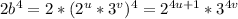
Согласно основной теореме арифметики, разложение числа на простые множители единственно. Поэтому можно приравнять соответствующие степени левой и правой частей равенства.
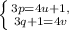
Легко подобрать минимальные подходящие решения:
p = 3, u = 2,
q = 1, v = 1.
Отсюда получим, что
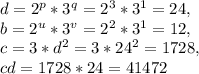
4/5 и 3/5 больше 5/9